8 Appendix
8.1 Linear algebra: definitions and results
Definition 8.1 (Eigenvalues) The eigenvalues of of a matrix \(M\) are the numbers \(\lambda\) for which: \[ |M - \lambda I| = 0, \] where \(| \bullet |\) is the determinant operator.
Proposition 8.1 (Properties of the determinant) We have:
- \(|MN|=|M|\times|N|\).
- \(|M^{-1}|=|M|^{-1}\).
- If \(M\) admits the diagonal representation \(M=TDT^{-1}\), where \(D\) is a diagonal matrix whose diagonal entries are \(\{\lambda_i\}_{i=1,\dots,n}\), then: \[ |M - \lambda I |=\prod_{i=1}^n (\lambda_i - \lambda). \]
Definition 8.2 (Moore-Penrose inverse) If \(M \in \mathbb{R}^{m \times n}\), then its Moore-Penrose pseudo inverse (exists and) is the unique matrix \(M^* \in \mathbb{R}^{n \times m}\) that satisfies:
- \(M M^* M = M\)
- \(M^* M M^* = M^*\)
- \((M M^*)'=M M^*\) .iv \((M^* M)'=M^* M\).
Proposition 8.2 (Properties of the Moore-Penrose inverse)
- If \(M\) is invertible then \(M^* = M^{-1}\).
- The pseudo-inverse of a zero matrix is its transpose. * The pseudo-inverse of the pseudo-inverse is the original matrix.
Definition 8.3 (Idempotent matrix) Matrix \(M\) is idempotent if \(M^2=M\).
If \(M\) is a symmetric idempotent matrix, then \(M'M=M\).
Proposition 8.3 (Roots of an idempotent matrix) The eigenvalues of an idempotent matrix are either 1 or 0.
Proof. If \(\lambda\) is an eigenvalue of an idempotent matrix \(M\) then \(\exists x \ne 0\) s.t. \(Mx=\lambda x\). Hence \(M^2x=\lambda M x \Rightarrow (1-\lambda)Mx=0\). Either all element of \(Mx\) are zero, in which case \(\lambda=0\) or at least one element of \(Mx\) is nonzero, in which case \(\lambda=1\).
Proposition 8.4 (Idempotent matrix and chi-square distribution) The rank of a symmetric idempotent matrix is equal to its trace.
Proof. The result follows from Prop. 8.3, combined with the fact that the rank of a symmetric matrix is equal to the number of its nonzero eigenvalues.
Proposition 8.5 (Constrained least squares) The solution of the following optimisation problem: \[\begin{eqnarray*} \underset{\boldsymbol\beta}{\min} && || \mathbf{y} - \mathbf{X}\boldsymbol\beta ||^2 \\ && \mbox{subject to } \mathbf{R}\boldsymbol\beta = \mathbf{q} \end{eqnarray*}\] is given by: \[ \boxed{\boldsymbol\beta^r = \boldsymbol\beta_0 - (\mathbf{X}'\mathbf{X})^{-1} \mathbf{R}'\{\mathbf{R}(\mathbf{X}'\mathbf{X})^{-1}\mathbf{R}'\}^{-1}(\mathbf{R}\boldsymbol\beta_0 - \mathbf{q}),} \] where \(\boldsymbol\beta_0=(\mathbf{X}'\mathbf{X})^{-1}\mathbf{X}'\mathbf{y}\).
Proof. See for instance Jackman, 2007.
Proposition 8.6 (Inverse of a partitioned matrix) We have: \[\begin{eqnarray*} &&\left[ \begin{array}{cc} \mathbf{A}_{11} & \mathbf{A}_{12} \\ \mathbf{A}_{21} & \mathbf{A}_{22} \end{array}\right]^{-1} = \\ &&\left[ \begin{array}{cc} (\mathbf{A}_{11} - \mathbf{A}_{12}\mathbf{A}_{22}^{-1}\mathbf{A}_{21})^{-1} & - \mathbf{A}_{11}^{-1}\mathbf{A}_{12}(\mathbf{A}_{22} - \mathbf{A}_{21}\mathbf{A}_{11}^{-1}\mathbf{A}_{12})^{-1} \\ -(\mathbf{A}_{22} - \mathbf{A}_{21}\mathbf{A}_{11}^{-1}\mathbf{A}_{12})^{-1}\mathbf{A}_{21}\mathbf{A}_{11}^{-1} & (\mathbf{A}_{22} - \mathbf{A}_{21}\mathbf{A}_{11}^{-1}\mathbf{A}_{12})^{-1} \end{array} \right]. \end{eqnarray*}\]
Definition 8.4 (Matrix derivatives) Consider a fonction \(f: \mathbb{R}^K \rightarrow \mathbb{R}\). Its first-order derivative is: \[ \frac{\partial f}{\partial \mathbf{b}}(\mathbf{b}) = \left[\begin{array}{c} \frac{\partial f}{\partial b_1}(\mathbf{b})\\ \vdots\\ \frac{\partial f}{\partial b_K}(\mathbf{b}) \end{array} \right]. \] We use the notation: \[ \frac{\partial f}{\partial \mathbf{b}'}(\mathbf{b}) = \left(\frac{\partial f}{\partial \mathbf{b}}(\mathbf{b})\right)'. \]
Proposition 8.7 We have:
- If \(f(\mathbf{b}) = A' \mathbf{b}\) where \(A\) is a \(K \times 1\) vector then \(\frac{\partial f}{\partial \mathbf{b}}(\mathbf{b}) = A\).
- If \(f(\mathbf{b}) = \mathbf{b}'A\mathbf{b}\) where \(A\) is a \(K \times K\) matrix, then \(\frac{\partial f}{\partial \mathbf{b}}(\mathbf{b}) = 2A\mathbf{b}\).
Proposition 8.8 (Square and absolute summability) We have: \[ \underbrace{\sum_{i=0}^{\infty}|\theta_i| < + \infty}_{\mbox{Absolute summability}} \Rightarrow \underbrace{\sum_{i=0}^{\infty} \theta_i^2 < + \infty}_{\mbox{Square summability}}. \]
Proof. See Appendix 3.A in Hamilton. Idea: Absolute summability implies that there exist \(N\) such that, for \(j>N\), \(|\theta_j| < 1\) (deduced from Cauchy criterion, Theorem 8.2 and therefore \(\theta_j^2 < |\theta_j|\).
8.2 Statistical analysis: definitions and results
8.2.1 Moments and statistics
Definition 8.5 (Partial correlation) The partial correlation between \(y\) and \(z\), controlling for some variables \(\mathbf{X}\) is the sample correlation between \(y^*\) and \(z^*\), where the latter two variables are the residuals in regressions of \(y\) on \(\mathbf{X}\) and of \(z\) on \(\mathbf{X}\), respectively.
This correlation is denoted by \(r_{yz}^\mathbf{X}\). By definition, we have: \[\begin{equation} r_{yz}^\mathbf{X} = \frac{\mathbf{z^*}'\mathbf{y^*}}{\sqrt{(\mathbf{z^*}'\mathbf{z^*})(\mathbf{y^*}'\mathbf{y^*})}}.\tag{8.1} \end{equation}\]
Definition 8.6 (Skewness and kurtosis) Let \(Y\) be a random variable whose fourth moment exists. The expectation of \(Y\) is denoted by \(\mu\).
- The skewness of \(Y\) is given by: \[ \frac{\mathbb{E}[(Y-\mu)^3]}{\{\mathbb{E}[(Y-\mu)^2]\}^{3/2}}. \]
- The kurtosis of \(Y\) is given by: \[ \frac{\mathbb{E}[(Y-\mu)^4]}{\{\mathbb{E}[(Y-\mu)^2]\}^{2}}. \]
Theorem 8.1 (Cauchy-Schwarz inequality) We have: \[ |\mathbb{C}ov(X,Y)| \le \sqrt{\mathbb{V}ar(X)\mathbb{V}ar(Y)} \] and, if \(X \ne =\) and \(Y \ne 0\), the equality holds iff \(X\) and \(Y\) are the same up to an affine transformation.
Proof. If \(\mathbb{V}ar(X)=0\), this is trivial. If this is not the case, then let’s define \(Z\) as \(Z = Y - \frac{\mathbb{C}ov(X,Y)}{\mathbb{V}ar(X)}X\). It is easily seen that \(\mathbb{C}ov(X,Z)=0\). Then, the variance of \(Y=Z+\frac{\mathbb{C}ov(X,Y)}{\mathbb{V}ar(X)}X\) is equal to the sum of the variance of \(Z\) and of the variance of \(\frac{\mathbb{C}ov(X,Y)}{\mathbb{V}ar(X)}X\), that is: \[ \mathbb{V}ar(Y) = \mathbb{V}ar(Z) + \left(\frac{\mathbb{C}ov(X,Y)}{\mathbb{V}ar(X)}\right)^2\mathbb{V}ar(X) \ge \left(\frac{\mathbb{C}ov(X,Y)}{\mathbb{V}ar(X)}\right)^2\mathbb{V}ar(X). \] The equality holds iff \(\mathbb{V}ar(Z)=0\), i.e. iff \(Y = \frac{\mathbb{C}ov(X,Y)}{\mathbb{V}ar(X)}X+cst\).
Definition 8.7 (Asymptotic level) An asymptotic test with critical region \(\Omega_n\) has an asymptotic level equal to \(\alpha\) if: \[ \underset{\theta \in \Theta}{\mbox{sup}} \quad \underset{n \rightarrow \infty}{\mbox{lim}} \mathbb{P}_\theta (S_n \in \Omega_n) = \alpha, \] where \(S_n\) is the test statistic and \(\Theta\) is such that the null hypothesis \(H_0\) is equivalent to \(\theta \in \Theta\).
Definition 8.8 (Asymptotically consistent test) An asymptotic test with critical region \(\Omega_n\) is consistent if: \[ \forall \theta \in \Theta^c, \quad \mathbb{P}_\theta (S_n \in \Omega_n) \rightarrow 1, \] where \(S_n\) is the test statistic and \(\Theta^c\) is such that the null hypothesis \(H_0\) is equivalent to \(\theta \notin \Theta^c\).
Definition 8.9 (Kullback discrepancy) Given two p.d.f. \(f\) and \(f^*\), the Kullback discrepancy is defined by: \[ I(f,f^*) = \mathbb{E}^* \left( \log \frac{f^*(Y)}{f(Y)} \right) = \int \log \frac{f^*(y)}{f(y)} f^*(y) dy. \]
Proposition 8.9 (Properties of the Kullback discrepancy) We have:
- \(I(f,f^*) \ge 0\)
- \(I(f,f^*) = 0\) iff \(f \equiv f^*\).
Proof. \(x \rightarrow -\log(x)\) is a convex function. Therefore \(\mathbb{E}^*(-\log f(Y)/f^*(Y)) \ge -\log \mathbb{E}^*(f(Y)/f^*(Y)) = 0\) (proves (i)). Since \(x \rightarrow -\log(x)\) is strictly convex, equality in (i) holds if and only if \(f(Y)/f^*(Y)\) is constant (proves (ii)).
Definition 8.10 (Characteristic function) For any real-valued random variable \(X\), the characteristic function is defined by: \[ \phi_X: u \rightarrow \mathbb{E}[\exp(iuX)]. \]
8.2.2 Standard distributions
Definition 8.11 (F distribution) Consider \(n=n_1+n_2\) i.i.d. \(\mathcal{N}(0,1)\) r.v. \(X_i\). If the r.v. \(F\) is defined by: \[ F = \frac{\sum_{i=1}^{n_1} X_i^2}{\sum_{j=n_1+1}^{n_1+n_2} X_j^2}\frac{n_2}{n_1} \] then \(F \sim \mathcal{F}(n_1,n_2)\). (See Table 8.4 for quantiles.)
Definition 8.12 (Student-t distribution) \(Z\) follows a Student-t (or \(t\)) distribution with \(\nu\) degrees of freedom (d.f.) if: \[ Z = X_0 \bigg/ \sqrt{\frac{\sum_{i=1}^{\nu}X_i^2}{\nu}}, \quad X_i \sim i.i.d. \mathcal{N}(0,1). \] We have \(\mathbb{E}(Z)=0\), and \(\mathbb{V}ar(Z)=\frac{\nu}{\nu-2}\) if \(\nu>2\). (See Table 8.2 for quantiles.)
Definition 8.13 (Chi-square distribution) \(Z\) follows a \(\chi^2\) distribution with \(\nu\) d.f. if \(Z = \sum_{i=1}^{\nu}X_i^2\) where \(X_i \sim i.i.d. \mathcal{N}(0,1)\). We have \(\mathbb{E}(Z)=\nu\). (See Table 8.3 for quantiles.)
Definition 8.14 (Cauchy distribution)
The probability distribution function of the Cauchy distribution defined by a location parameter \(\mu\) and a scale parameter \(\gamma\) is: \[ f(x) = \frac{1}{\pi \gamma \left(1 + \left[\frac{x-\mu}{\gamma}\right]^2\right)}. \] The mean and variance of this distribution are undefined.
Figure 8.1: Pdf of the Cauchy distribution (\(\mu=0\), \(\gamma=1\)).
Proposition 8.10 (Inner product of a multivariate Gaussian variable) Let \(X\) be a \(n\)-dimensional multivariate Gaussian variable: \(X \sim \mathcal{N}(0,\Sigma)\). We have: \[ X' \Sigma^{-1}X \sim \chi^2(n). \]
Proof. Because \(\Sigma\) is a symmetrical definite positive matrix, it admits the spectral decomposition \(PDP'\) where \(P\) is an orthogonal matrix (i.e. \(PP'=Id\)) and D is a diagonal matrix with non-negative entries. Denoting by \(\sqrt{D^{-1}}\) the diagonal matrix whose diagonal entries are the inverse of those of \(D\), it is easily checked that the covariance matrix of \(Y:=\sqrt{D^{-1}}P'X\) is \(Id\). Therefore \(Y\) is a vector of uncorrelated Gaussian variables. The properties of Gaussian variables imply that the components of \(Y\) are then also independent. Hence \(Y'Y=\sum_i Y_i^2 \sim \chi^2(n)\).
It remains to note that \(Y'Y=X'PD^{-1}P'X=X'\mathbb{V}ar(X)^{-1}X\) to conclude.
Definition 8.15 (Generalized Extreme Value (GEV) distribution) The vector of disturbances \(\boldsymbol\varepsilon=[\varepsilon_{1,1},\dots,\varepsilon_{1,K_1},\dots,\varepsilon_{J,1},\dots,\varepsilon_{J,K_J}]'\) follows the Generalized Extreme Value (GEV) distribution if its c.d.f. is: \[ F(\boldsymbol\varepsilon,\boldsymbol\rho) = \exp(-G(e^{-\varepsilon_{1,1}},\dots,e^{-\varepsilon_{J,K_J}};\boldsymbol\rho)) \] with \[\begin{eqnarray*} G(\mathbf{Y};\boldsymbol\rho) &\equiv& G(Y_{1,1},\dots,Y_{1,K_1},\dots,Y_{J,1},\dots,Y_{J,K_J};\boldsymbol\rho) \\ &=& \sum_{j=1}^J\left(\sum_{k=1}^{K_j} Y_{jk}^{1/\rho_j} \right)^{\rho_j} \end{eqnarray*}\]
8.2.3 Stochastic convergences
Proposition 8.11 (Chebychev's inequality) If \(\mathbb{E}(|X|^r)\) is finite for some \(r>0\) then: \[ \forall \varepsilon > 0, \quad \mathbb{P}(|X - c|>\varepsilon) \le \frac{\mathbb{E}[|X - c|^r]}{\varepsilon^r}. \] In particular, for \(r=2\): \[ \forall \varepsilon > 0, \quad \mathbb{P}(|X - c|>\varepsilon) \le \frac{\mathbb{E}[(X - c)^2]}{\varepsilon^2}. \]
Proof. Remark that \(\varepsilon^r \mathbb{I}_{\{|X| \ge \varepsilon\}} \le |X|^r\) and take the expectation of both sides.
Definition 8.16 (Convergence in probability) The random variable sequence \(x_n\) converges in probability to a constant \(c\) if \(\forall \varepsilon\), \(\lim_{n \rightarrow \infty} \mathbb{P}(|x_n - c|>\varepsilon) = 0\).
It is denoted as: \(\mbox{plim } x_n = c\).
Definition 8.17 (Convergence in the Lr norm) \(x_n\) converges in the \(r\)-th mean (or in the \(L^r\)-norm) towards \(x\), if \(\mathbb{E}(|x_n|^r)\) and \(\mathbb{E}(|x|^r)\) exist and if \[ \lim_{n \rightarrow \infty} \mathbb{E}(|x_n - x|^r) = 0. \] It is denoted as: \(x_n \overset{L^r}{\rightarrow} c\).
For \(r=2\), this convergence is called mean square convergence.
Definition 8.18 (Almost sure convergence) The random variable sequence \(x_n\) converges almost surely to \(c\) if \(\mathbb{P}(\lim_{n \rightarrow \infty} x_n = c) = 1\).
It is denoted as: \(x_n \overset{a.s.}{\rightarrow} c\).
Definition 8.19 (Convergence in distribution) \(x_n\) is said to converge in distribution (or in law) to \(x\) if \[ \lim_{n \rightarrow \infty} F_{x_n}(s) = F_{x}(s) \] for all \(s\) at which \(F_X\) –the cumulative distribution of \(X\)– is continuous.
It is denoted as: \(x_n \overset{d}{\rightarrow} x\).
Proposition 8.12 (Rules for limiting distributions (Slutsky)) We have:
Slutsky’s theorem: If \(x_n \overset{d}{\rightarrow} x\) and \(y_n \overset{p}{\rightarrow} c\) then \[\begin{eqnarray*} x_n y_n &\overset{d}{\rightarrow}& x c \\ x_n + y_n &\overset{d}{\rightarrow}& x + c \\ x_n/y_n &\overset{d}{\rightarrow}& x / c \quad (\mbox{if }c \ne 0) \end{eqnarray*}\]
Continuous mapping theorem: If \(x_n \overset{d}{\rightarrow} x\) and \(g\) is a continuous function then \(g(x_n) \overset{d}{\rightarrow} g(x).\)
Proposition 8.13 (Implications of stochastic convergences) We have: \[\begin{align*} &\boxed{\overset{L^s}{\rightarrow}}& &\underset{1 \le r \le s}{\Rightarrow}& &\boxed{\overset{L^r}{\rightarrow}}&\\ && && &\Downarrow&\\ &\boxed{\overset{a.s.}{\rightarrow}}& &\Rightarrow& &\boxed{\overset{p}{\rightarrow}}& \Rightarrow \qquad \boxed{\overset{d}{\rightarrow}}. \end{align*}\]
Proof. (of the fact that \(\left(\overset{p}{\rightarrow}\right) \Rightarrow \left( \overset{d}{\rightarrow}\right)\)). Assume that \(X_n \overset{p}{\rightarrow} X\). Denoting by \(F\) and \(F_n\) the c.d.f. of \(X\) and \(X_n\), respectively: \[\begin{eqnarray*} F_n(x) &=& \mathbb{P}(X_n \le x,X\le x+\varepsilon) + \mathbb{P}(X_n \le x,X > x+\varepsilon)\\ &\le& F(x+\varepsilon) + \mathbb{P}(|X_n - X|>\varepsilon).\tag{8.2} \end{eqnarray*}\] Besides, \[\begin{eqnarray*} F(x-\varepsilon) &=& \mathbb{P}(X \le x-\varepsilon,X_n \le x) + \mathbb{P}(X \le x-\varepsilon,X_n > x)\\ &\le& F_n(x) + \mathbb{P}(|X_n - X|>\varepsilon), \end{eqnarray*}\] which implies: \[\begin{equation} F(x-\varepsilon) - \mathbb{P}(|X_n - X|>\varepsilon) \le F_n(x).\tag{8.3} \end{equation}\] Eqs. (8.2) and (8.3) imply: \[ F(x-\varepsilon) - \mathbb{P}(|X_n - X|>\varepsilon) \le F_n(x) \le F(x+\varepsilon) + \mathbb{P}(|X_n - X|>\varepsilon). \] Taking limits as \(n \rightarrow \infty\) yields \[ F(x-\varepsilon) \le \underset{n \rightarrow \infty}{\mbox{lim inf}}\; F_n(x) \le \underset{n \rightarrow \infty}{\mbox{lim sup}}\; F_n(x) \le F(x+\varepsilon). \] The result is then obtained by taking limits as \(\varepsilon \rightarrow 0\) (if \(F\) is continuous at \(x\)).
Proposition 8.14 (Convergence in distribution to a constant) If \(X_n\) converges in distribution to a constant \(c\), then \(X_n\) converges in probability to \(c\).
Proof. If \(\varepsilon>0\), we have \(\mathbb{P}(X_n < c - \varepsilon) \underset{n \rightarrow \infty}{\rightarrow} 0\) i.e. \(\mathbb{P}(X_n \ge c - \varepsilon) \underset{n \rightarrow \infty}{\rightarrow} 1\) and \(\mathbb{P}(X_n < c + \varepsilon) \underset{n \rightarrow \infty}{\rightarrow} 1\). Therefore \(\mathbb{P}(c - \varepsilon \le X_n < c + \varepsilon) \underset{n \rightarrow \infty}{\rightarrow} 1\), which gives the result.
Example 8.1 (Convergence in probability but not $L^r$) Let \(\{x_n\}_{n \in \mathbb{N}}\) be a series of random variables defined by: \[ x_n = n u_n, \] where \(u_n\) are independent random variables s.t. \(u_n \sim \mathcal{B}(1/n)\).
We have \(x_n \overset{p}{\rightarrow} 0\) but \(x_n \overset{L^r}{\nrightarrow} 0\) because \(\mathbb{E}(|X_n-0|)=\mathbb{E}(X_n)=1\).
Theorem 8.2 (Cauchy criterion (non-stochastic case)) We have that \(\sum_{i=0}^{T} a_i\) converges (\(T \rightarrow \infty\)) iff, for any \(\eta > 0\), there exists an integer \(N\) such that, for all \(M\ge N\), \[ \left|\sum_{i=N+1}^{M} a_i\right| < \eta. \]
Theorem 8.3 (Cauchy criterion (stochastic case)) We have that \(\sum_{i=0}^{T} \theta_i \varepsilon_{t-i}\) converges in mean square (\(T \rightarrow \infty\)) to a random variable iff, for any \(\eta > 0\), there exists an integer \(N\) such that, for all \(M\ge N\), \[ \mathbb{E}\left[\left(\sum_{i=N+1}^{M} \theta_i \varepsilon_{t-i}\right)^2\right] < \eta. \]
8.2.4 Central limit theorem
Theorem 8.4 (Law of large numbers) The sample mean is a consistent estimator of the population mean.
Proof. Let’s denote by \(\phi_{X_i}\) the characteristic function of a r.v. \(X_i\). If the mean of \(X_i\) is \(\mu\) then the Talyor expansion of the characteristic function is: \[ \phi_{X_i}(u) = \mathbb{E}(\exp(iuX)) = 1 + iu\mu + o(u). \] The properties of the characteristic function (see Def. 8.10) imply that: \[ \phi_{\frac{1}{n}(X_1+\dots+X_n)}(u) = \prod_{i=1}^{n} \left(1 + i\frac{u}{n}\mu + o\left(\frac{u}{n}\right) \right) \rightarrow e^{iu\mu}. \] The facts that (a) \(e^{iu\mu}\) is the characteristic function of the constant \(\mu\) and (b) that a characteristic function uniquely characterises a distribution imply that the sample mean converges in distribution to the constant \(\mu\), which further implies that it converges in probability to \(\mu\).
Theorem 8.5 (Lindberg-Levy Central limit theorem, CLT) If \(x_n\) is an i.i.d. sequence of random variables with mean \(\mu\) and variance \(\sigma^2\) (\(\in ]0,+\infty[\)), then: \[ \boxed{\sqrt{n} (\bar{x}_n - \mu) \overset{d}{\rightarrow} \mathcal{N}(0,\sigma^2), \quad \mbox{where} \quad \bar{x}_n = \frac{1}{n} \sum_{i=1}^{n} x_i.} \]
Proof. Let us introduce the r.v. \(Y_n:= \sqrt{n}(\bar{X}_n - \mu)\). We have \(\phi_{Y_n}(u) = \left[ \mathbb{E}\left( \exp(i \frac{1}{\sqrt{n}} u (X_1 - \mu)) \right) \right]^n\). We have: \[\begin{eqnarray*} &&\left[ \mathbb{E}\left( \exp\left(i \frac{1}{\sqrt{n}} u (X_1 - \mu)\right) \right) \right]^n\\ &=& \left[ \mathbb{E}\left( 1 + i \frac{1}{\sqrt{n}} u (X_1 - \mu) - \frac{1}{2n} u^2 (X_1 - \mu)^2 + o(u^2) \right) \right]^n \\ &=& \left( 1 - \frac{1}{2n}u^2\sigma^2 + o(u^2)\right)^n. \end{eqnarray*}\] Therefore \(\phi_{Y_n}(u) \underset{n \rightarrow \infty}{\rightarrow} \exp \left( - \frac{1}{2}u^2\sigma^2 \right)\), which is the characteristic function of \(\mathcal{N}(0,\sigma^2)\).
8.3 Some properties of Gaussian variables
Proposition 8.15 If \(\mathbf{A}\) is idempotent and if \(\mathbf{x}\) is Gaussian, \(\mathbf{L}\mathbf{x}\) and \(\mathbf{x}'\mathbf{A}\mathbf{x}\) are independent if \(\mathbf{L}\mathbf{A}=\mathbf{0}\).
Proof. If \(\mathbf{L}\mathbf{A}=\mathbf{0}\), then the two Gaussian vectors \(\mathbf{L}\mathbf{x}\) and \(\mathbf{A}\mathbf{x}\) are independent. This implies the independence of any function of \(\mathbf{L}\mathbf{x}\) and any function of \(\mathbf{A}\mathbf{x}\). The results then follows from the observation that \(\mathbf{x}'\mathbf{A}\mathbf{x}=(\mathbf{A}\mathbf{x})'(\mathbf{A}\mathbf{x})\), which is a function of \(\mathbf{A}\mathbf{x}\).
Proposition 8.16 (Bayesian update in a vector of Gaussian variables) If \[ \left[ \begin{array}{c} Y_1\\ Y_2 \end{array} \right] \sim \mathcal{N} \left(0, \left[\begin{array}{cc} \Omega_{11} & \Omega_{12}\\ \Omega_{21} & \Omega_{22} \end{array}\right] \right), \] then \[ Y_{2}|Y_{1} \sim \mathcal{N} \left( \Omega_{21}\Omega_{11}^{-1}Y_{1},\Omega_{22}-\Omega_{21}\Omega_{11}^{-1}\Omega_{12} \right). \] \[ Y_{1}|Y_{2} \sim \mathcal{N} \left( \Omega_{12}\Omega_{22}^{-1}Y_{2},\Omega_{11}-\Omega_{12}\Omega_{22}^{-1}\Omega_{21} \right). \]
Proposition 8.17 (Truncated distributions) If \(X\) is a random variable distributed according to some p.d.f. \(f\), with c.d.f. \(F\), with infinite support. Then the p.d.f. of \(X|a \le X < b\) is \[ g(x) = \frac{f(x)}{F(b)-F(a)}\mathbb{I}_{\{a \le x < b\}}, \] for any \(a<b\).
In partiucular, for a Gaussian variable \(X \sim \mathcal{N}(\mu,\sigma^2)\), we have \[ f(X=x|a\le X<b) = \dfrac{\dfrac{1}{\sigma}\phi\left(\dfrac{x - \mu}{\sigma}\right)}{Z}. \] with \(Z = \Phi(\beta)-\Phi(\alpha)\), where \(\alpha = \dfrac{a - \mu}{\sigma}\) and \(\beta = \dfrac{b - \mu}{\sigma}\).
Moreover: \[\begin{eqnarray} \mathbb{E}(X|a\le X<b) &=& \mu - \frac{\phi\left(\beta\right)-\phi\left(\alpha\right)}{Z}\sigma. \tag{8.4} \end{eqnarray}\]
We also have: \[\begin{eqnarray} && \mathbb{V}ar(X|a\le X<b) \nonumber\\ &=& \sigma^2\left[ 1 - \frac{\beta\phi\left(\beta\right)-\alpha\phi\left(\alpha\right)}{Z} - \left(\frac{\phi\left(\beta\right)-\phi\left(\alpha\right)}{Z}\right)^2 \right] \tag{8.5} \end{eqnarray}\]
In particular, for \(b \rightarrow \infty\), we get: \[\begin{equation} \mathbb{V}ar(X|a < X) = \sigma^2\left[1 + \alpha\lambda(-\alpha) - \lambda(-\alpha)^2 \right], \tag{8.6} \end{equation}\] with \(\lambda(x)=\dfrac{\phi(x)}{\Phi(x)}\) is called the inverse Mills ratio.
Consider the case where \(a \rightarrow - \infty\) (i.e. the conditioning set is \(X<b\)) and \(\mu=0\), \(\sigma=1\). Then Eq. (8.4) gives \(\mathbb{E}(X|X<b) = - \lambda(b) = - \dfrac{\phi(b)}{\Phi(b)}\), where \(\lambda\) is the function computing the inverse Mills ratio.
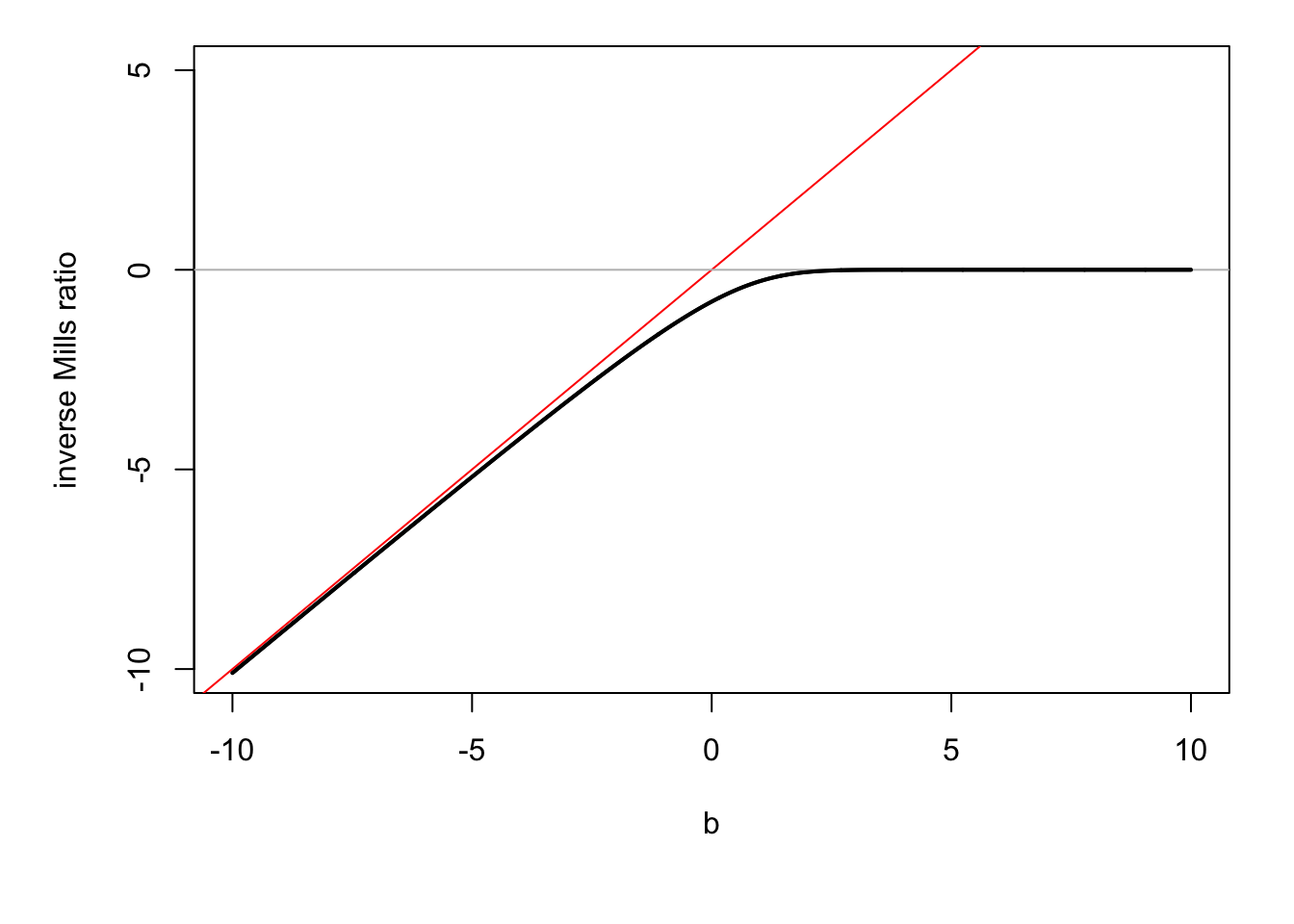
Figure 8.2: \(\mathbb{E}(X|X<b)\) as a function of \(b\) when \(X\sim \mathcal{N}(0,1)\) (in black).
Proposition 8.18 (p.d.f. of a multivariate Gaussian variable) If \(Y \sim \mathcal{N}(\mu,\Omega)\) and if \(Y\) is a \(n\)-dimensional vector, then the density function of \(Y\) is: \[ \frac{1}{(2 \pi)^{n/2}|\Omega|^{1/2}}\exp\left[-\frac{1}{2}\left(Y-\mu\right)'\Omega^{-1}\left(Y-\mu\right)\right]. \]
8.4 Proofs
Proof of Proposition 3.4
Proof. Assumptions (i) and (ii) (in the set of Assumptions 3.1) imply that \(\boldsymbol\theta_{MLE}\) exists (\(=\mbox{argmax}_\theta (1/n)\log \mathcal{L}(\boldsymbol\theta;\mathbf{y})\)).
\((1/n)\log \mathcal{L}(\boldsymbol\theta;\mathbf{y})\) can be interpreted as the sample mean of the r.v. \(\log f(Y_i;\boldsymbol\theta)\) that are i.i.d. Therefore \((1/n)\log \mathcal{L}(\boldsymbol\theta;\mathbf{y})\) converges to \(\mathbb{E}_{\boldsymbol\theta_0}(\log f(Y;\boldsymbol\theta))\) – which exists (Assumption iv).
Because the latter convergence is uniform (Assumption v), the solution \(\boldsymbol\theta_{MLE}\) almost surely converges to the solution to the limit problem: \[ \mbox{argmax}_\theta \mathbb{E}_{\boldsymbol\theta_0}(\log f(Y;\boldsymbol\theta)) = \mbox{argmax}_\theta \int_{\mathcal{Y}} \log f(y;\boldsymbol\theta)f(y;\boldsymbol\theta_0) dy. \]
Properties of the Kullback information measure (see Prop. 8.9), together with the identifiability assumption (ii) implies that the solution to the limit problem is unique and equal to \(\boldsymbol\theta_0\).
Consider a r.v. sequence \(\boldsymbol\theta\) that converges to \(\boldsymbol\theta_0\). The Taylor expansion of the score in a neighborood of \(\boldsymbol\theta_0\) yields to: \[ \frac{\partial \log \mathcal{L}(\boldsymbol\theta;\mathbf{y})}{\partial \boldsymbol\theta} = \frac{\partial \log \mathcal{L}(\boldsymbol\theta_0;\mathbf{y})}{\partial \boldsymbol\theta} + \frac{\partial^2 \log \mathcal{L}(\boldsymbol\theta_0;\mathbf{y})}{\partial \boldsymbol\theta \partial \boldsymbol\theta'}(\boldsymbol\theta - \boldsymbol\theta_0) + o_p(\boldsymbol\theta - \boldsymbol\theta_0) \]
\(\boldsymbol\theta_{MLE}\) converges to \(\boldsymbol\theta_0\) and satisfies the likelihood equation \(\frac{\partial \log \mathcal{L}(\boldsymbol\theta;\mathbf{y})}{\partial \boldsymbol\theta} = \mathbf{0}\). Therefore: \[ \frac{\partial \log \mathcal{L}(\boldsymbol\theta_0;\mathbf{y})}{\partial \boldsymbol\theta} \approx - \frac{\partial^2 \log \mathcal{L}(\boldsymbol\theta_0;\mathbf{y})}{\partial \boldsymbol\theta \partial \boldsymbol\theta'}(\boldsymbol\theta_{MLE} - \boldsymbol\theta_0), \] or equivalently: \[ \frac{1}{\sqrt{n}} \frac{\partial \log \mathcal{L}(\boldsymbol\theta_0;\mathbf{y})}{\partial \boldsymbol\theta} \approx \left(- \frac{1}{n} \sum_{i=1}^n \frac{\partial^2 \log f(y_i;\boldsymbol\theta_0)}{\partial \boldsymbol\theta \partial \boldsymbol\theta'} \right)\sqrt{n}(\boldsymbol\theta_{MLE} - \boldsymbol\theta_0), \]
By the law of large numbers, we have: \(\left(- \frac{1}{n} \sum_{i=1}^n \frac{\partial^2 \log f(y_i;\boldsymbol\theta_0)}{\partial \boldsymbol\theta \partial \boldsymbol\theta'} \right) \overset{}\rightarrow \frac{1}{n} \mathbf{I}(\boldsymbol\theta_0) = \mathcal{I}_Y(\boldsymbol\theta_0)\).
Besides, we have: \[\begin{eqnarray*} \frac{1}{\sqrt{n}} \frac{\partial \log \mathcal{L}(\boldsymbol\theta_0;\mathbf{y})}{\partial \boldsymbol\theta} &=& \sqrt{n} \left( \frac{1}{n} \sum_i \frac{\partial \log f(y_i;\boldsymbol\theta_0)}{\partial \boldsymbol\theta} \right) \\ &=& \sqrt{n} \left( \frac{1}{n} \sum_i \left\{ \frac{\partial \log f(y_i;\boldsymbol\theta_0)}{\partial \boldsymbol\theta} - \mathbb{E}_{\boldsymbol\theta_0} \frac{\partial \log f(Y_i;\boldsymbol\theta_0)}{\partial \boldsymbol\theta} \right\} \right) \end{eqnarray*}\] which converges to \(\mathcal{N}(0,\mathcal{I}_Y(\boldsymbol\theta_0))\) by the CLT.
Collecting the preceding results leads to (b). The fact that \(\boldsymbol\theta_{MLE}\) achieves the FDCR bound proves (c).
Proof of Proposition 3.5
Proof. We have \(\sqrt{n}(\hat{\boldsymbol\theta}_{n} - \boldsymbol\theta_{0}) \overset{d}{\rightarrow} \mathcal{N}(0,\mathcal{I}(\boldsymbol\theta_0)^{-1})\) (Eq. (3.9)). A Taylor expansion around \(\boldsymbol\theta_0\) yields to: \[\begin{equation} \sqrt{n}(h(\hat{\boldsymbol\theta}_{n}) - h(\boldsymbol\theta_{0})) \overset{d}{\rightarrow} \mathcal{N}\left(0,\frac{\partial h(\boldsymbol\theta_{0})}{\partial \boldsymbol\theta'}\mathcal{I}(\boldsymbol\theta_0)^{-1}\frac{\partial h(\boldsymbol\theta_{0})'}{\partial \boldsymbol\theta}\right). \tag{8.7} \end{equation}\] Under \(H_0\), \(h(\boldsymbol\theta_{0})=0\) therefore: \[\begin{equation} \sqrt{n} h(\hat{\boldsymbol\theta}_{n}) \overset{d}{\rightarrow} \mathcal{N}\left(0,\frac{\partial h(\boldsymbol\theta_{0})}{\partial \boldsymbol\theta'}\mathcal{I}(\boldsymbol\theta_0)^{-1}\frac{\partial h(\boldsymbol\theta_{0})'}{\partial \boldsymbol\theta}\right). \tag{8.8} \end{equation}\] Hence \[ \sqrt{n} \left( \frac{\partial h(\boldsymbol\theta_{0})}{\partial \boldsymbol\theta'}\mathcal{I}(\boldsymbol\theta_0)^{-1}\frac{\partial h(\boldsymbol\theta_{0})'}{\partial \boldsymbol\theta} \right)^{-1/2} h(\hat{\boldsymbol\theta}_{n}) \overset{d}{\rightarrow} \mathcal{N}\left(0,Id\right). \] Taking the quadratic form, we obtain: \[ n h(\hat{\boldsymbol\theta}_{n})' \left( \frac{\partial h(\boldsymbol\theta_{0})}{\partial \boldsymbol\theta'}\mathcal{I}(\boldsymbol\theta_0)^{-1}\frac{\partial h(\boldsymbol\theta_{0})'}{\partial \boldsymbol\theta} \right)^{-1} h(\hat{\boldsymbol\theta}_{n}) \overset{d}{\rightarrow} \chi^2(r). \]
The fact that the test has asymptotic level \(\alpha\) directly stems from what precedes. Consistency of the test: Consider \(\theta_0 \in \Theta\). Because the MLE is consistent, \(h(\hat{\boldsymbol\theta}_{n})\) converges to \(h(\boldsymbol\theta_0) \ne 0\). Eq. (8.7) is still valid. It implies that \(\xi^W_n\) converges to \(+\infty\) and therefore that \(\mathbb{P}_{\boldsymbol\theta}(\xi^W_n \ge \chi^2_{1-\alpha}(r)) \rightarrow 1\).
Proof of Proposition 3.6
Proof. Notations: “\(\approx\)” means “equal up to a term that converges to 0 in probability”. We are under \(H_0\). \(\hat{\boldsymbol\theta}^0\) is the constrained ML estimator; \(\hat{\boldsymbol\theta}\) denotes the unconstrained one.
We combine the two Taylor expansion: \(h(\hat{\boldsymbol\theta}_n) \approx \dfrac{\partial h(\boldsymbol\theta_0)}{\partial \boldsymbol\theta'}(\hat{\boldsymbol\theta}_n - \boldsymbol\theta_0)\) and \(h(\hat{\boldsymbol\theta}_n^0) \approx \dfrac{\partial h(\boldsymbol\theta_0)}{\partial \boldsymbol\theta'}(\hat{\boldsymbol\theta}_n^0 - \boldsymbol\theta_0)\) and we use \(h(\hat{\boldsymbol\theta}_n^0)=0\) (by definition) to get: \[\begin{equation} \sqrt{n}h(\hat{\boldsymbol\theta}_n) \approx \dfrac{\partial h(\boldsymbol\theta_0)}{\partial \boldsymbol\theta'}\sqrt{n}(\hat{\boldsymbol\theta}_n - \hat{\boldsymbol\theta}^0_n). \tag{8.9} \end{equation}\] Besides, we have (using the definition of the information matrix): \[\begin{equation} \frac{1}{\sqrt{n}}\frac{\partial \log \mathcal{L}(\hat{\boldsymbol\theta}^0_n;\mathbf{y})}{\partial \boldsymbol\theta} \approx \frac{1}{\sqrt{n}}\frac{\partial \log \mathcal{L}(\boldsymbol\theta_0;\mathbf{y})}{\partial \boldsymbol\theta} - \mathcal{I}(\boldsymbol\theta_0)\sqrt{n}(\hat{\boldsymbol\theta}^0_n-\boldsymbol\theta_0) \tag{8.10} \end{equation}\] and: \[\begin{equation} 0=\frac{1}{\sqrt{n}}\frac{\partial \log \mathcal{L}(\hat{\boldsymbol\theta}_n;\mathbf{y})}{\partial \boldsymbol\theta} \approx \frac{1}{\sqrt{n}}\frac{\partial \log \mathcal{L}(\boldsymbol\theta_0;\mathbf{y})}{\partial \boldsymbol\theta} - \mathcal{I}(\boldsymbol\theta_0)\sqrt{n}(\hat{\boldsymbol\theta}_n-\boldsymbol\theta_0).\tag{8.11} \end{equation}\] Taking the difference and multiplying by \(\mathcal{I}(\boldsymbol\theta_0)^{-1}\): \[\begin{equation} \sqrt{n}(\hat{\boldsymbol\theta}_n-\hat{\boldsymbol\theta}_n^0) \approx \mathcal{I}(\boldsymbol\theta_0)^{-1}\frac{1}{\sqrt{n}}\frac{\partial \log \mathcal{L}(\hat{\boldsymbol\theta}^0_n;\mathbf{y})}{\partial \boldsymbol\theta} \mathcal{I}(\boldsymbol\theta_0).\tag{8.12} \end{equation}\] Eqs. (8.9) and (8.12) yield to: \[\begin{equation} \sqrt{n}h(\hat{\boldsymbol\theta}_n) \approx \dfrac{\partial h(\boldsymbol\theta_0)}{\partial \boldsymbol\theta'} \mathcal{I}(\boldsymbol\theta_0)^{-1}\frac{1}{\sqrt{n}}\frac{\partial \log \mathcal{L}(\hat{\boldsymbol\theta}^0_n;\mathbf{y})}{\partial \boldsymbol\theta}.\tag{8.13} \end{equation}\]
Recall that \(\hat{\boldsymbol\theta}^0_n\) is the MLE of \(\boldsymbol\theta_0\) under the constraint \(h(\boldsymbol\theta)=0\). The vector of Lagrange multipliers \(\hat\lambda_n\) associated to this program satisfies: \[\begin{equation} \frac{\partial \log \mathcal{L}(\hat{\boldsymbol\theta}^0_n;\mathbf{y})}{\partial \boldsymbol\theta}+ \frac{\partial h'(\hat{\boldsymbol\theta}^0_n;\mathbf{y})}{\partial \boldsymbol\theta}\hat\lambda_n = 0.\tag{8.14} \end{equation}\] Substituting the latter equation in Eq. (8.13) gives: \[\begin{eqnarray*} \sqrt{n}h(\hat{\boldsymbol\theta}_n) &\approx& - \dfrac{\partial h(\boldsymbol\theta_0)}{\partial \boldsymbol\theta'} \mathcal{I}(\boldsymbol\theta_0)^{-1} \frac{\partial h'(\hat{\boldsymbol\theta}^0_n;\mathbf{y})}{\partial \boldsymbol\theta} \frac{\hat\lambda_n}{\sqrt{n}} \\ &\approx& - \dfrac{\partial h(\boldsymbol\theta_0)}{\partial \boldsymbol\theta'} \mathcal{I}(\boldsymbol\theta_0)^{-1} \frac{\partial h'(\boldsymbol\theta_0;\mathbf{y})}{\partial \boldsymbol\theta} \frac{\hat\lambda_n}{\sqrt{n}}, \end{eqnarray*}\] which yields: \[\begin{equation} \frac{\hat\lambda_n}{\sqrt{n}} \approx - \left( \dfrac{\partial h(\boldsymbol\theta_0)}{\partial \boldsymbol\theta'} \mathcal{I}(\boldsymbol\theta_0)^{-1} \frac{\partial h'(\boldsymbol\theta_0;\mathbf{y})}{\partial \boldsymbol\theta} \right)^{-1} \sqrt{n}h(\hat{\boldsymbol\theta}_n).\tag{8.15} \end{equation}\] It follows, from Eq. (8.8), that: \[ \frac{\hat\lambda_n}{\sqrt{n}} \overset{d}{\rightarrow} \mathcal{N}\left(0,\left( \dfrac{\partial h(\boldsymbol\theta_0)}{\partial \boldsymbol\theta'} \mathcal{I}(\boldsymbol\theta_0)^{-1} \frac{\partial h'(\boldsymbol\theta_0;\mathbf{y})}{\partial \boldsymbol\theta} \right)^{-1}\right). \] Taking the quadratic form of the last equation gives: \[ \frac{1}{n}\hat\lambda_n' \dfrac{\partial h(\hat{\boldsymbol\theta}^0_n)}{\partial \boldsymbol\theta'} \mathcal{I}(\hat{\boldsymbol\theta}^0_n)^{-1} \frac{\partial h'(\hat{\boldsymbol\theta}^0_n;\mathbf{y})}{\partial \boldsymbol\theta} \hat\lambda_n \overset{d}{\rightarrow} \chi^2(r). \] Using Eq. (8.14), it appears that the left-hand side term of the last equation is \(\xi^{LM}\) as defined in Eq. (3.15). Consistency: see Remark 17.3 in Gouriéroux and Monfort (1995).
Proof of Proposition 3.7
Proof. Let us first demonstrate the asymptotic equivalence of \(\xi^{LM}\) and \(\xi^{LR}\).
The second-order Taylor expansions of \(\log \mathcal{L}(\hat{\boldsymbol\theta}^0_n,\mathbf{y})\) and \(\log \mathcal{L}(\hat{\boldsymbol\theta}_n,\mathbf{y})\) are: \[\begin{eqnarray*} \log \mathcal{L}(\hat{\boldsymbol\theta}_n,\mathbf{y}) &\approx& \log \mathcal{L}(\boldsymbol\theta_0,\mathbf{y}) + \frac{\partial \log \mathcal{L}(\boldsymbol\theta_0,\mathbf{y})}{\partial \boldsymbol\theta'}(\hat{\boldsymbol\theta}_n-\boldsymbol\theta_0) \\ && - \frac{n}{2} (\hat{\boldsymbol\theta}_n-\boldsymbol\theta_0)' \mathcal{I}(\boldsymbol\theta_0) (\hat{\boldsymbol\theta}_n-\boldsymbol\theta_0)\\ \log \mathcal{L}(\hat{\boldsymbol\theta}^0_n,\mathbf{y}) &\approx& \log \mathcal{L}(\boldsymbol\theta_0,\mathbf{y}) + \frac{\partial \log \mathcal{L}(\boldsymbol\theta_0,\mathbf{y})}{\partial \boldsymbol\theta'}(\hat{\boldsymbol\theta}^0_n-\boldsymbol\theta_0) \\ && - \frac{n}{2} (\hat{\boldsymbol\theta}^0_n-\boldsymbol\theta_0)' \mathcal{I}(\boldsymbol\theta_0) (\hat{\boldsymbol\theta}^0_n-\boldsymbol\theta_0). \end{eqnarray*}\] Taking the difference, we obtain: \[\begin{eqnarray*} \xi_n^{LR} &\approx& 2\frac{\partial \log \mathcal{L}(\boldsymbol\theta_0,\mathbf{y})}{\partial \boldsymbol\theta'} (\hat{\boldsymbol\theta}_n-\hat{\boldsymbol\theta}^0_n) + n (\hat{\boldsymbol\theta}^0_n-\boldsymbol\theta_0)' \mathcal{I}(\boldsymbol\theta_0) (\hat{\boldsymbol\theta}^0_n-\boldsymbol\theta_0)\\ && - n (\hat{\boldsymbol\theta}_n-\boldsymbol\theta_0)' \mathcal{I}(\boldsymbol\theta_0) (\hat{\boldsymbol\theta}_n-\boldsymbol\theta_0). \end{eqnarray*}\] Using \(\dfrac{1}{\sqrt{n}}\frac{\partial \log \mathcal{L}(\boldsymbol\theta_0;\mathbf{y})}{\partial \boldsymbol\theta} \approx \mathcal{I}(\boldsymbol\theta_0)\sqrt{n}(\hat{\boldsymbol\theta}_n-\boldsymbol\theta_0)\) (Eq. (8.11)), we have: \[\begin{eqnarray*} \xi_n^{LR} &\approx& 2n(\hat{\boldsymbol\theta}_n-\boldsymbol\theta_0)'\mathcal{I}(\boldsymbol\theta_0) (\hat{\boldsymbol\theta}_n-\hat{\boldsymbol\theta}^0_n) + n (\hat{\boldsymbol\theta}^0_n-\boldsymbol\theta_0)' \mathcal{I}(\boldsymbol\theta_0) (\hat{\boldsymbol\theta}^0_n-\boldsymbol\theta_0) \\ && - n (\hat{\boldsymbol\theta}_n-\boldsymbol\theta_0)' \mathcal{I}(\boldsymbol\theta_0) (\hat{\boldsymbol\theta}_n-\boldsymbol\theta_0). \end{eqnarray*}\] In the second of the three terms in the sum, we replace \((\hat{\boldsymbol\theta}^0_n-\boldsymbol\theta_0)\) by \((\hat{\boldsymbol\theta}^0_n-\hat{\boldsymbol\theta}_n+\hat{\boldsymbol\theta}_n-\boldsymbol\theta_0)\) and we develop the associated product. This leads to: \[\begin{equation} \xi_n^{LR} \approx n (\hat{\boldsymbol\theta}^0_n-\hat{\boldsymbol\theta}_n)' \mathcal{I}(\boldsymbol\theta_0)^{-1} (\hat{\boldsymbol\theta}^0_n-\hat{\boldsymbol\theta}_n). \tag{8.16} \end{equation}\] The difference between Eqs. (8.10) and (8.11) implies: \[ \frac{1}{\sqrt{n}}\frac{\partial \log \mathcal{L}(\hat{\boldsymbol\theta}^0_n;\mathbf{y})}{\partial \boldsymbol\theta} \approx \mathcal{I}(\boldsymbol\theta_0)\sqrt{n}(\hat{\boldsymbol\theta}_n-\hat{\boldsymbol\theta}^0_n), \] which, associated to Eq. @(eq:lr10), gives: \[ \xi_n^{LR} \approx \frac{1}{n} \frac{\partial \log \mathcal{L}(\hat{\boldsymbol\theta}^0_n;\mathbf{y})}{\partial \boldsymbol\theta'} \mathcal{I}(\boldsymbol\theta_0)^{-1} \frac{\partial \log \mathcal{L}(\hat{\boldsymbol\theta}^0_n;\mathbf{y})}{\partial \boldsymbol\theta} \approx \xi_n^{LM}. \] Hence \(\xi_n^{LR}\) has the same asymptotic distribution as \(\xi_n^{LM}\).
Let’s show that the LR test is consistent. For this, note that: \[\begin{eqnarray*} \frac{\log \mathcal{L}(\hat{\boldsymbol\theta},\mathbf{y}) - \log \mathcal{L}(\hat{\boldsymbol\theta}^0,\mathbf{y})}{n} &=& \frac{1}{n} \sum_{i=1}^n[\log f(y_i;\hat{\boldsymbol\theta}_n) - \log f(y_i;\hat{\boldsymbol\theta}_n^0)]\\ &\rightarrow& \mathbb{E}_0[\log f(Y;\boldsymbol\theta_0) - \log f(Y;\boldsymbol\theta_\infty)], \end{eqnarray*}\] where \(\boldsymbol\theta_\infty\), the pseudo true value, is such that \(h(\boldsymbol\theta_\infty) \ne 0\) (by definition of \(H_1\)). From the Kullback inequality and the asymptotic identifiability of \(\boldsymbol\theta_0\), it follows that \(\mathbb{E}_0[\log f(Y;\boldsymbol\theta_0) - \log f(Y;\boldsymbol\theta_\infty)] >0\). Therefore \(\xi_n^{LR} \rightarrow + \infty\) under \(H_1\).
Let us now demonstrate the equivalence of \(\xi^{LM} and \xi^{W}\).
We have (using Eq. (eq:multiplier)): \[ \xi^{LM}_n = \frac{1}{n}\hat\lambda_n' \dfrac{\partial h(\hat{\boldsymbol\theta}^0_n)}{\partial \boldsymbol\theta'} \mathcal{I}(\hat{\boldsymbol\theta}^0_n)^{-1} \frac{\partial h'(\hat{\boldsymbol\theta}^0_n;\mathbf{y})}{\partial \boldsymbol\theta} \hat\lambda_n. \] Since, under \(H_0\), \(\hat{\boldsymbol\theta}_n^0\approx\hat{\boldsymbol\theta}_n \approx {\boldsymbol\theta}_0\), Eq. (8.15) therefore implies that: \[ \xi^{LM} \approx n h(\hat{\boldsymbol\theta}_n)' \left( \dfrac{\partial h(\hat{\boldsymbol\theta}_n)}{\partial \boldsymbol\theta'} \mathcal{I}(\hat{\boldsymbol\theta}_n)^{-1} \frac{\partial h'(\hat{\boldsymbol\theta}_n;\mathbf{y})}{\partial \boldsymbol\theta} \right)^{-1} h(\hat{\boldsymbol\theta}_n) = \xi^{W}, \] which gives the result.
8.5 Additional codes
8.5.1 Simulating GEV distributions
The following lines of code have been used to generate Figure 5.2.
n.sim <- 4000
par(mfrow=c(1,3),
plt=c(.2,.95,.2,.85))
all.rhos <- c(.3,.6,.95)
for(j in 1:length(all.rhos)){
theta <- 1/all.rhos[j]
v1 <- runif(n.sim)
v2 <- runif(n.sim)
w <- rep(.000001,n.sim)
# solve for f(w) = w*(1 - log(w)/theta) - v2 = 0
for(i in 1:20){
f.i <- w * (1 - log(w)/theta) - v2
f.prime <- 1 - log(w)/theta - 1/theta
w <- w - f.i/f.prime
}
u1 <- exp(v1^(1/theta) * log(w))
u2 <- exp((1-v1)^(1/theta) * log(w))
# Get eps1 and eps2 using the inverse of
# the Gumbel distribution's cdf:
eps1 <- -log(-log(u1))
eps2 <- -log(-log(u2))
cbind(cor(eps1,eps2),1-all.rhos[j]^2)
plot(eps1,eps2,pch=19,col="#FF000044",
main=paste("rho = ",toString(all.rhos[j]),sep=""),
xlab=expression(epsilon[1]),
ylab=expression(epsilon[2]),
cex.lab=2,cex.main=1.5)
}8.6 Statistical Tables
| 0 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.5000 | 0.6179 | 0.7257 | 0.8159 | 0.8849 | 0.9332 | 0.9641 | 0.9821 | 0.9918 | 0.9965 |
| 0.1 | 0.5040 | 0.6217 | 0.7291 | 0.8186 | 0.8869 | 0.9345 | 0.9649 | 0.9826 | 0.9920 | 0.9966 |
| 0.2 | 0.5080 | 0.6255 | 0.7324 | 0.8212 | 0.8888 | 0.9357 | 0.9656 | 0.9830 | 0.9922 | 0.9967 |
| 0.3 | 0.5120 | 0.6293 | 0.7357 | 0.8238 | 0.8907 | 0.9370 | 0.9664 | 0.9834 | 0.9925 | 0.9968 |
| 0.4 | 0.5160 | 0.6331 | 0.7389 | 0.8264 | 0.8925 | 0.9382 | 0.9671 | 0.9838 | 0.9927 | 0.9969 |
| 0.5 | 0.5199 | 0.6368 | 0.7422 | 0.8289 | 0.8944 | 0.9394 | 0.9678 | 0.9842 | 0.9929 | 0.9970 |
| 0.6 | 0.5239 | 0.6406 | 0.7454 | 0.8315 | 0.8962 | 0.9406 | 0.9686 | 0.9846 | 0.9931 | 0.9971 |
| 0.7 | 0.5279 | 0.6443 | 0.7486 | 0.8340 | 0.8980 | 0.9418 | 0.9693 | 0.9850 | 0.9932 | 0.9972 |
| 0.8 | 0.5319 | 0.6480 | 0.7517 | 0.8365 | 0.8997 | 0.9429 | 0.9699 | 0.9854 | 0.9934 | 0.9973 |
| 0.9 | 0.5359 | 0.6517 | 0.7549 | 0.8389 | 0.9015 | 0.9441 | 0.9706 | 0.9857 | 0.9936 | 0.9974 |
| 1 | 0.5398 | 0.6554 | 0.7580 | 0.8413 | 0.9032 | 0.9452 | 0.9713 | 0.9861 | 0.9938 | 0.9974 |
| 1.1 | 0.5438 | 0.6591 | 0.7611 | 0.8438 | 0.9049 | 0.9463 | 0.9719 | 0.9864 | 0.9940 | 0.9975 |
| 1.2 | 0.5478 | 0.6628 | 0.7642 | 0.8461 | 0.9066 | 0.9474 | 0.9726 | 0.9868 | 0.9941 | 0.9976 |
| 1.3 | 0.5517 | 0.6664 | 0.7673 | 0.8485 | 0.9082 | 0.9484 | 0.9732 | 0.9871 | 0.9943 | 0.9977 |
| 1.4 | 0.5557 | 0.6700 | 0.7704 | 0.8508 | 0.9099 | 0.9495 | 0.9738 | 0.9875 | 0.9945 | 0.9977 |
| 1.5 | 0.5596 | 0.6736 | 0.7734 | 0.8531 | 0.9115 | 0.9505 | 0.9744 | 0.9878 | 0.9946 | 0.9978 |
| 1.6 | 0.5636 | 0.6772 | 0.7764 | 0.8554 | 0.9131 | 0.9515 | 0.9750 | 0.9881 | 0.9948 | 0.9979 |
| 1.7 | 0.5675 | 0.6808 | 0.7794 | 0.8577 | 0.9147 | 0.9525 | 0.9756 | 0.9884 | 0.9949 | 0.9979 |
| 1.8 | 0.5714 | 0.6844 | 0.7823 | 0.8599 | 0.9162 | 0.9535 | 0.9761 | 0.9887 | 0.9951 | 0.9980 |
| 1.9 | 0.5753 | 0.6879 | 0.7852 | 0.8621 | 0.9177 | 0.9545 | 0.9767 | 0.9890 | 0.9952 | 0.9981 |
| 2 | 0.5793 | 0.6915 | 0.7881 | 0.8643 | 0.9192 | 0.9554 | 0.9772 | 0.9893 | 0.9953 | 0.9981 |
| 2.1 | 0.5832 | 0.6950 | 0.7910 | 0.8665 | 0.9207 | 0.9564 | 0.9778 | 0.9896 | 0.9955 | 0.9982 |
| 2.2 | 0.5871 | 0.6985 | 0.7939 | 0.8686 | 0.9222 | 0.9573 | 0.9783 | 0.9898 | 0.9956 | 0.9982 |
| 2.3 | 0.5910 | 0.7019 | 0.7967 | 0.8708 | 0.9236 | 0.9582 | 0.9788 | 0.9901 | 0.9957 | 0.9983 |
| 2.4 | 0.5948 | 0.7054 | 0.7995 | 0.8729 | 0.9251 | 0.9591 | 0.9793 | 0.9904 | 0.9959 | 0.9984 |
| 2.5 | 0.5987 | 0.7088 | 0.8023 | 0.8749 | 0.9265 | 0.9599 | 0.9798 | 0.9906 | 0.9960 | 0.9984 |
| 2.6 | 0.6026 | 0.7123 | 0.8051 | 0.8770 | 0.9279 | 0.9608 | 0.9803 | 0.9909 | 0.9961 | 0.9985 |
| 2.7 | 0.6064 | 0.7157 | 0.8078 | 0.8790 | 0.9292 | 0.9616 | 0.9808 | 0.9911 | 0.9962 | 0.9985 |
| 2.8 | 0.6103 | 0.7190 | 0.8106 | 0.8810 | 0.9306 | 0.9625 | 0.9812 | 0.9913 | 0.9963 | 0.9986 |
| 2.9 | 0.6141 | 0.7224 | 0.8133 | 0.8830 | 0.9319 | 0.9633 | 0.9817 | 0.9916 | 0.9964 | 0.9986 |
| 0.05 | 0.1 | 0.75 | 0.9 | 0.95 | 0.975 | 0.99 | 0.999 | |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.079 | 0.158 | 2.414 | 6.314 | 12.706 | 25.452 | 63.657 | 636.619 |
| 2 | 0.071 | 0.142 | 1.604 | 2.920 | 4.303 | 6.205 | 9.925 | 31.599 |
| 3 | 0.068 | 0.137 | 1.423 | 2.353 | 3.182 | 4.177 | 5.841 | 12.924 |
| 4 | 0.067 | 0.134 | 1.344 | 2.132 | 2.776 | 3.495 | 4.604 | 8.610 |
| 5 | 0.066 | 0.132 | 1.301 | 2.015 | 2.571 | 3.163 | 4.032 | 6.869 |
| 6 | 0.065 | 0.131 | 1.273 | 1.943 | 2.447 | 2.969 | 3.707 | 5.959 |
| 7 | 0.065 | 0.130 | 1.254 | 1.895 | 2.365 | 2.841 | 3.499 | 5.408 |
| 8 | 0.065 | 0.130 | 1.240 | 1.860 | 2.306 | 2.752 | 3.355 | 5.041 |
| 9 | 0.064 | 0.129 | 1.230 | 1.833 | 2.262 | 2.685 | 3.250 | 4.781 |
| 10 | 0.064 | 0.129 | 1.221 | 1.812 | 2.228 | 2.634 | 3.169 | 4.587 |
| 20 | 0.063 | 0.127 | 1.185 | 1.725 | 2.086 | 2.423 | 2.845 | 3.850 |
| 30 | 0.063 | 0.127 | 1.173 | 1.697 | 2.042 | 2.360 | 2.750 | 3.646 |
| 40 | 0.063 | 0.126 | 1.167 | 1.684 | 2.021 | 2.329 | 2.704 | 3.551 |
| 50 | 0.063 | 0.126 | 1.164 | 1.676 | 2.009 | 2.311 | 2.678 | 3.496 |
| 60 | 0.063 | 0.126 | 1.162 | 1.671 | 2.000 | 2.299 | 2.660 | 3.460 |
| 70 | 0.063 | 0.126 | 1.160 | 1.667 | 1.994 | 2.291 | 2.648 | 3.435 |
| 80 | 0.063 | 0.126 | 1.159 | 1.664 | 1.990 | 2.284 | 2.639 | 3.416 |
| 90 | 0.063 | 0.126 | 1.158 | 1.662 | 1.987 | 2.280 | 2.632 | 3.402 |
| 100 | 0.063 | 0.126 | 1.157 | 1.660 | 1.984 | 2.276 | 2.626 | 3.390 |
| 200 | 0.063 | 0.126 | 1.154 | 1.653 | 1.972 | 2.258 | 2.601 | 3.340 |
| 500 | 0.063 | 0.126 | 1.152 | 1.648 | 1.965 | 2.248 | 2.586 | 3.310 |
| 0.05 | 0.1 | 0.75 | 0.9 | 0.95 | 0.975 | 0.99 | 0.999 | |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.004 | 0.016 | 1.323 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| 2 | 0.103 | 0.211 | 2.773 | 4.605 | 5.991 | 7.378 | 9.210 | 13.816 |
| 3 | 0.352 | 0.584 | 4.108 | 6.251 | 7.815 | 9.348 | 11.345 | 16.266 |
| 4 | 0.711 | 1.064 | 5.385 | 7.779 | 9.488 | 11.143 | 13.277 | 18.467 |
| 5 | 1.145 | 1.610 | 6.626 | 9.236 | 11.070 | 12.833 | 15.086 | 20.515 |
| 6 | 1.635 | 2.204 | 7.841 | 10.645 | 12.592 | 14.449 | 16.812 | 22.458 |
| 7 | 2.167 | 2.833 | 9.037 | 12.017 | 14.067 | 16.013 | 18.475 | 24.322 |
| 8 | 2.733 | 3.490 | 10.219 | 13.362 | 15.507 | 17.535 | 20.090 | 26.124 |
| 9 | 3.325 | 4.168 | 11.389 | 14.684 | 16.919 | 19.023 | 21.666 | 27.877 |
| 10 | 3.940 | 4.865 | 12.549 | 15.987 | 18.307 | 20.483 | 23.209 | 29.588 |
| 20 | 10.851 | 12.443 | 23.828 | 28.412 | 31.410 | 34.170 | 37.566 | 45.315 |
| 30 | 18.493 | 20.599 | 34.800 | 40.256 | 43.773 | 46.979 | 50.892 | 59.703 |
| 40 | 26.509 | 29.051 | 45.616 | 51.805 | 55.758 | 59.342 | 63.691 | 73.402 |
| 50 | 34.764 | 37.689 | 56.334 | 63.167 | 67.505 | 71.420 | 76.154 | 86.661 |
| 60 | 43.188 | 46.459 | 66.981 | 74.397 | 79.082 | 83.298 | 88.379 | 99.607 |
| 70 | 51.739 | 55.329 | 77.577 | 85.527 | 90.531 | 95.023 | 100.425 | 112.317 |
| 80 | 60.391 | 64.278 | 88.130 | 96.578 | 101.879 | 106.629 | 112.329 | 124.839 |
| 90 | 69.126 | 73.291 | 98.650 | 107.565 | 113.145 | 118.136 | 124.116 | 137.208 |
| 100 | 77.929 | 82.358 | 109.141 | 118.498 | 124.342 | 129.561 | 135.807 | 149.449 |
| 200 | 168.279 | 174.835 | 213.102 | 226.021 | 233.994 | 241.058 | 249.445 | 267.541 |
| 500 | 449.147 | 459.926 | 520.950 | 540.930 | 553.127 | 563.852 | 576.493 | 603.446 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| alpha = 0.9 | ||||||||||
| 5 | 4.060 | 3.780 | 3.619 | 3.520 | 3.453 | 3.405 | 3.368 | 3.339 | 3.316 | 3.297 |
| 10 | 3.285 | 2.924 | 2.728 | 2.605 | 2.522 | 2.461 | 2.414 | 2.377 | 2.347 | 2.323 |
| 15 | 3.073 | 2.695 | 2.490 | 2.361 | 2.273 | 2.208 | 2.158 | 2.119 | 2.086 | 2.059 |
| 20 | 2.975 | 2.589 | 2.380 | 2.249 | 2.158 | 2.091 | 2.040 | 1.999 | 1.965 | 1.937 |
| 50 | 2.809 | 2.412 | 2.197 | 2.061 | 1.966 | 1.895 | 1.840 | 1.796 | 1.760 | 1.729 |
| 100 | 2.756 | 2.356 | 2.139 | 2.002 | 1.906 | 1.834 | 1.778 | 1.732 | 1.695 | 1.663 |
| 500 | 2.716 | 2.313 | 2.095 | 1.956 | 1.859 | 1.786 | 1.729 | 1.683 | 1.644 | 1.612 |
| alpha = 0.95 | ||||||||||
| 5 | 6.608 | 5.786 | 5.409 | 5.192 | 5.050 | 4.950 | 4.876 | 4.818 | 4.772 | 4.735 |
| 10 | 4.965 | 4.103 | 3.708 | 3.478 | 3.326 | 3.217 | 3.135 | 3.072 | 3.020 | 2.978 |
| 15 | 4.543 | 3.682 | 3.287 | 3.056 | 2.901 | 2.790 | 2.707 | 2.641 | 2.588 | 2.544 |
| 20 | 4.351 | 3.493 | 3.098 | 2.866 | 2.711 | 2.599 | 2.514 | 2.447 | 2.393 | 2.348 |
| 50 | 4.034 | 3.183 | 2.790 | 2.557 | 2.400 | 2.286 | 2.199 | 2.130 | 2.073 | 2.026 |
| 100 | 3.936 | 3.087 | 2.696 | 2.463 | 2.305 | 2.191 | 2.103 | 2.032 | 1.975 | 1.927 |
| 500 | 3.860 | 3.014 | 2.623 | 2.390 | 2.232 | 2.117 | 2.028 | 1.957 | 1.899 | 1.850 |
| alpha = 0.99 | ||||||||||
| 5 | 16.258 | 13.274 | 12.060 | 11.392 | 10.967 | 10.672 | 10.456 | 10.289 | 10.158 | 10.051 |
| 10 | 10.044 | 7.559 | 6.552 | 5.994 | 5.636 | 5.386 | 5.200 | 5.057 | 4.942 | 4.849 |
| 15 | 8.683 | 6.359 | 5.417 | 4.893 | 4.556 | 4.318 | 4.142 | 4.004 | 3.895 | 3.805 |
| 20 | 8.096 | 5.849 | 4.938 | 4.431 | 4.103 | 3.871 | 3.699 | 3.564 | 3.457 | 3.368 |
| 50 | 7.171 | 5.057 | 4.199 | 3.720 | 3.408 | 3.186 | 3.020 | 2.890 | 2.785 | 2.698 |
| 100 | 6.895 | 4.824 | 3.984 | 3.513 | 3.206 | 2.988 | 2.823 | 2.694 | 2.590 | 2.503 |
| 500 | 6.686 | 4.648 | 3.821 | 3.357 | 3.054 | 2.838 | 2.675 | 2.547 | 2.443 | 2.356 |