3 Estimation Methods

This chapter presents three approaches to estimate parametric models: the General Method of Moments (GMM), the Maximum Likelihood approach (ML), and the Bayesian approach. The general context is the following: You observe a sample \(\mathbf{y}=\{y_1,\dots,y_n\}\), you assume that these data have been generated by a model parameterized by \({\boldsymbol\theta} \in \mathbb{R}^K\), and you want to estimate this vector \({\boldsymbol\theta}_0\).

3.1 Generalized Method of Moments (GMM)

3.1.1 Definition of the GMM estimator

We denote by \(y_i\) a \(p \times 1\) vector of variables; by \(\boldsymbol\theta\) an \(K \times 1\) vector of parameters, and by \(h(y_i;\boldsymbol\theta)\) a continuous \(r \times 1\) vector-valued function.

We denote by \(\boldsymbol\theta_0\) the true value of \(\boldsymbol\theta\) and we assume that \(\boldsymbol\theta_0\) satisfies: \[ \mathbb{E}[h(y_i;\boldsymbol\theta_0)] = \mathbf{0}. \]

We denote by \(\underline{y_i}\) the information contained in the current and past observations of \(y_i\), that is: \(\underline{y_i} = \{y_i,y_{i-1},\dots,y_1\}\). We denote by \(g(\underline{y_n};\boldsymbol\theta)\) the sample average of the \(h(y_i;\boldsymbol\theta)\) vectors, i.e.: \[ g(\underline{y_n};\boldsymbol\theta) = \frac{1}{n} \sum_{i=1}^{n} h(y_i;\boldsymbol\theta). \]

The intuition behind the GMM estimator is the following: choose \(\boldsymbol\theta\) so as to make the sample moment as close as possible to their population values, that is 0.

Definition 3.1 A GMM estimator of \(\boldsymbol\theta_0\) is given by: \[ \hat{\boldsymbol\theta}_n = \mbox{argmin}_{\boldsymbol\theta} \quad g(\underline{y_n};\boldsymbol\theta)'\, W_n \, g(\underline{y_n};\boldsymbol\theta), \] where \(W_n\) is a positive definite matrix (that may depend on \(\underline{y_n}\)).

In the specific case where \(K = r\) (the dimension of \(\boldsymbol\theta\) is the same as that of \(h(y_i;\boldsymbol\theta)\) —or of \(g(\underline{y_n};\boldsymbol\theta)\)— then \(\hat{\boldsymbol\theta}_n\) satisfies: \[ g(\underline{y_n};\hat{\boldsymbol\theta}_n) = \mathbf{0}. \] Under regularity and identification conditions, this estimator is consistent, that is \(\hat{\boldsymbol\theta}_{n}\) converges towards \(\boldsymbol\theta_0\) in probability, which we denote by: \[\begin{equation} \mbox{plim}_n\;\hat{\boldsymbol\theta}_{n}= \boldsymbol\theta_0,\quad \mbox{or} \quad\hat{\boldsymbol\theta}_{n} \overset{p}{\rightarrow} \boldsymbol\theta_0,\tag{3.1} \end{equation}\] i.e. \(\forall \varepsilon>0\), \(\lim_{n \rightarrow \infty} \mathbb{P}(|\hat{\boldsymbol\theta}_{n} - \boldsymbol\theta_0|>\varepsilon) = 0\) (this is Definition 8.16).

Definition 3.1 involves a positive definite matrix \(W_n\). While one can take any positive definite matrix to have consistency (Eq. (3.1)), it can be shown that he GMM estimator achieves the minimum asymptotic variance when \(W_n\) is the inverse of matrix \(S\), the latter being defined by: \[ S = Asy.\mathbb{V}ar\left(\sqrt{n}g(\underline{y_n};\hat{\boldsymbol\theta}_n)\right). \] In this case, \(W_n\) is said to be the optimal weighting matrix.

The intuition behind this result is the same that underlies Generalized Least Squares (see Section 1.5.2), that is: it is beneficial to use a criterion in which the weights are inversely proportional to the variances of the moments.

If \(h(x_i;\boldsymbol\theta_0)\) is not correlated to \(h(x_j;\boldsymbol\theta_0)\), for \(i \ne j\), then we have: \[ S = \mathbb{V}ar(h(x_i;\boldsymbol\theta_0)), \] which can be approximated by \[ \hat{\Gamma}_{0,n}=\frac{1}{n}\sum_{i=1}^{n} h(x_i;\hat{\boldsymbol\theta}_n)h(x_{i};\hat{\boldsymbol\theta}_n)'. \]

In a time series context, we often have correlation between \(x_i\) and \(x_{i+k}\), especially for small \(k\)’s. In this case, and if the time series \(\{y_i\}\) is covariance stationary, then we have: \[ S := \sum_{\nu = -\infty}^{\infty} \Gamma_\nu, \] where \(\Gamma_\nu := \mathbb{E}[h(x_i;\boldsymbol\theta_0) h(x_{i-\nu};\boldsymbol\theta_0)']\). Matrix \(S\) is called the long-run variance of process \(\{y_i\}\).

For \(\nu \ge 0\), let us define \(\hat{\Gamma}_{\nu,n}\) by: \[ \hat{\Gamma}_{\nu,n} = \frac{1}{n} \sum_{i=\nu + 1}^{n} h(x_i;\hat{\boldsymbol\theta}_n)h(x_{i-\nu};\hat{\boldsymbol\theta}_n)', \] then \(S\) can be approximated by the Newey and West (1987) formula: \[\begin{equation} \hat{\Gamma}_{0,n} + \sum_{\nu=1}^{q}\left[1-\frac{\nu}{q+1}\right](\hat{\Gamma}_{\nu,n}+\hat{\Gamma}_{\nu,n}'). \tag{3.2} \end{equation}\]

3.1.2 Asymptotic distribution of the GMM estimator

We have: \[\begin{equation} \boxed{\sqrt{n}(\hat{\boldsymbol\theta}_n - \boldsymbol\theta_0) \overset{d}{\rightarrow} \mathcal{N}(0,V),}\tag{3.3} \end{equation}\] where \(V = (DS^{-1}D')^{-1}\), with \[ D := \left.\mathbb{E}\left(\frac{\partial h(x_i;\boldsymbol\theta)}{\partial \boldsymbol\theta'}\right)\right|_{\boldsymbol\theta = \boldsymbol\theta_0}. \]

Matrix \(V\) can be approximated by \[\begin{equation} \hat{V}_n = (\hat{D}_n\hat{S}_n^{-1}\hat{D}_n')^{-1},\tag{3.4} \end{equation}\] where \(\hat{S}_n\) is given by Eq. (3.2) and \[ \hat{D}'_n := \left.\frac{\partial g(\underline{y_n};\boldsymbol\theta)}{\partial \boldsymbol\theta'}\right|_{\boldsymbol\theta = \hat{\boldsymbol\theta}_n}. \] In practice, the previous matrix is computed numerically.

3.1.3 Testing hypotheses in the GMM framework

A first important test is the one concerning the validity of the moment restrictions (Sargan-Hansen test; Sargan (1958) and Hansen (1982)). Assume that the number of restrictions imposed is larger than the number of parameters to estimate (\(r>K\)). In this case, the restrictions are said to be over-identifiying.

Under correct specification, we asymptotically have: \[ \sqrt{n}g(\underline{y_n};{\boldsymbol\theta}_0) \sim \mathcal{N}(0,S). \] As a result, it comes that: \[\begin{equation} J_n = \left(\sqrt{n}g(\underline{y_n};{\boldsymbol\theta}_0)\right)'S^{-1}\left(\sqrt{n}g(\underline{y_n};{\boldsymbol\theta}_0)\right) \tag{3.5} \end{equation}\] asymptotically follows a \(\chi^2\) distribution. The number of degrees of freedom is equal to \(r-K\). (Note that, for \(r=K\), we have, as expected, \(J=0\).) That is, asymptotically: \[ J_n \sim \chi^2(r-K). \] The GMM framework also allows to easily test linear restrictions on the parameters. First, given Eq. (3.3), Wald tests (see Eq. (1.13) in Section 1.2.5) are readily available. Second, one can also resort to a test equivalent to the likelihood ratio tests (see Definition 3.8). More precisely, consider an unconstrained model and a constrained version of this model, the number of restrictions being equal to \(k\). If the two models are estimated by considering the same moment constraints, and the same weighting matrix —using Eq. (3.4), based on the unrestricted model—, then we have that: \[ n \left[(g(\underline{y_n};\hat{{\boldsymbol\theta}}^*_n)-g(\underline{y_n};\hat{{\boldsymbol\theta}}_n)\right] \sim \chi^2(k), \] where \(\hat{{\boldsymbol\theta}}^*_n\) is the constrained estimate of \({\boldsymbol\theta}_0\).

3.1.4 Example: Estimation of the Stochastic Discount Factor (s.d.f.)

Under the no-arbitrage assumption, there exists a random variable \(\mathcal{M}_{t,t+1}\) (a s.d.f.) such that \[ \mathbb{E}_t(\mathcal{M}_{t,t+1}R_{t+1})=1 \] for any (gross) asset return \(R_t\). In the following, \(R_t\) denotes a \(n_r\)-dimensional vector of gross returns.

We consider the following specification of the s.d.f.: \[\begin{equation} \mathcal{M}_{t,t+1} = 1 - \textbf{b}_M'(F_{t+1} - \mathbb{E}_t(F_{t+1})), \tag{3.6} \end{equation}\] where \(F_t\) is a vector of factors. Eq. (3.6) then reads: \[ \mathbb{E}_t([1 - \textbf{b}_M'(F_{t+1} - \mathbb{E}_t(F_{t+1}))]R_{t+1})=1. \]

Assume that the date-\(t\) information set is \(\mathcal{I}_t=\{\textbf{z}_t,\mathcal{I}_{t-1}\}\), where \(\textbf{z}_t\) is a vector of variables observed on date \(t\). (We then have \(\mathbb{E}_t(\bullet) \equiv \mathbb{E}(\bullet|\mathcal{I}_t)\).)

We can use \(\textbf{z}_t\) as an instrument. Indeed, we have: \[\begin{eqnarray} &&\mathbb{E}(z_{i,t} [\textbf{b}_M'\{F_{t+1} - \mathbb{E}_t(F_{t+1})\}R_{t+1}-R_{t+1}+1]) \nonumber \\ &=&\mathbb{E}(\mathbb{E}_t\{z_{i,t} [\textbf{b}_M'\{F_{t+1} - \mathbb{E}_t(F_{t+1})\}R_{t+1}-R_{t+1}+1]\})\nonumber\\ &=&\mathbb{E}(z_{i,t} \underbrace{\mathbb{E}_t\{\textbf{b}_M'\{F_{t+1} - \mathbb{E}_t(F_{t+1})\}R_{t+1}-R_{t+1}+1\}}_{1 - \mathbb{E}_t(\mathcal{M}_{t,t+1}R_{t+1})=0})=0.\tag{3.7} \end{eqnarray}\] We have then converted a conditional moment condition into a unconditional one (which we need to implement the GMM approach described above). However, at that stage, we can still not directly use the GMM formulas because of the conditional expectation \(\mathbb{E}_t(F_{t+1})\) that appears in \(\mathbb{E}(z_{i,t} [\textbf{b}_M'\{F_{t+1} - \mathbb{E}_t(F_{t+1})\}R_{t+1}-R_{t+1}+1])=0\).

To go further, let us assume that: \[ \mathbb{E}_t(F_{t+1}) = \textbf{b}_F \textbf{z}_t. \] We can then easily estimate matrix \(\textbf{b}_F\) (of dimension \(n_F \times n_z\)) by OLS. Note here that these OLS can be seen as a special GMM case. Indeed, as was done in Eq. (3.7), we can show that, for the \(j^{th}\) component of \(F_t\), we have: \[ \mathbb{E}( [F_{j,t+1} - \textbf{b}_{F,j} \textbf{z}_t]\textbf{z}_{t})=0, \] where \(\textbf{b}_{F,j}\) denotes the \(j^{th}\) row of \(\textbf{b}_{F}\). This yields the OLS formula.

Equipped with \(\textbf{b}_F\), we rely on the following moment restrictions to estimate \(\textbf{b}_M\): \[ \mathbb{E}(z_{i,t} [\textbf{b}_M'\{F_{t+1} - \textbf{b}_F \textbf{z}_t\}R_{t+1}-R_{t+1}+1])=0. \] Specifically, the number of restrictions is \(n_R \times n_z\). Let us implement this approach in the U.S. context, using data extracted from the FRED database. In factor \(F_t\), we use the changes in the VIX and in the personal consumption expenditures. The returns (\(R_t\)) are based on the Wilshire 5000 Price Index (a stock price index) and on the ICE BofA BBB US Corporate Index Total Return Index (a bond return index).

library(fredr)
fredr_set_key("df65e14c054697a52b4511e77fcfa1f3")
start_date <- as.Date("1990-01-01"); end_date <- as.Date("2022-01-01")
f <- function(ticker){
  fredr(series_id = ticker,
        observation_start = start_date,observation_end = end_date,
        frequency = "m",aggregation_method = "avg")
}
vix <- f("VIXCLS") # VIX
pce <- f("PCE") # Personal consumption expenditures
sto <- f("WILL5000PRFC") # Wilshire 5000 Full Cap Price Index
bdr <- f("BAMLCC0A4BBBTRIV") # ICE BofA BBB US Corp. Index Tot. Return
T <- dim(vix)[1]
dvix <- c(vix$value[3:T]/vix$value[2:(T-1)]) # change in VIX t+1
dpce <- c(pce$value[3:T]/pce$value[2:(T-1)]) # change in PCE t+1
dsto <- c(sto$value[3:T]/sto$value[2:(T-1)]) # return t+1
dbdr <- c(bdr$value[3:T]/bdr$value[2:(T-1)]) # return t+1
dvix_1 <- c(vix$value[2:(T-1)]/vix$value[1:(T-2)]) # change in VIX t
dpce_1 <- c(pce$value[2:(T-1)]/pce$value[1:(T-2)]) # change in PCE t
dsto_1 <- c(sto$value[2:(T-1)]/sto$value[1:(T-2)]) # return t
dbdr_1 <- c(bdr$value[2:(T-1)]/bdr$value[1:(T-2)]) # return t

Define the matrices containing the \(F_{t+1}\), \(\textbf{z}_t\), and \(R_{t+1}\) vectors:

F_tp1 <- cbind(dvix,dpce)
Z     <- cbind(1,dvix_1,dpce_1,dsto_1,dbdr_1)
b_F <- t(solve(t(Z) %*% Z) %*% t(Z) %*% F_tp1)
F_innov <- F_tp1 - Z %*% t(b_F)
R_tp1 <- cbind(dsto,dbdr)
n_F <- dim(F_tp1)[2]; n_R <- dim(R_tp1)[2]; n_z <- dim(Z)[2]

Function f_aux compute the \(h(x_t;{\boldsymbol\theta})\) and the \(g(\underline{y_T};{\boldsymbol\theta})\); function f2beMin is the function to be minimized.

f_aux <- function(theta){
  b_M <- matrix(theta[1:n_F],ncol=1)
  R_aux <- matrix(F_innov %*% b_M,T-2,n_R) * R_tp1 - R_tp1 + 1
  H <- (R_aux %x% matrix(1,1,n_z)) * (matrix(1,1,n_R) %x% Z)
  g <- matrix(apply(H,2,mean),ncol=1)
  return(list(g=g,H=H))
}
f2beMin <- function(theta,W){# function to be minimized
  res <- f_aux(theta)
  return(t(res$g) %*% W %*% res$g)
}

Now, let’s minimize this function, using use the BFGS numerical algorithm (part of the optim wrapper). We run 5 iterations (where \(W\) is updated).

library(AEC)
theta <- c(rep(0,n_F)) # inital value
for(i in 1:10){# recursion on W
  res <- f_aux(theta)
  W <-  solve(NW.LongRunVariance(res$H,q=6))
  res.optim <- optim(theta,f2beMin,W=W,
                     method="BFGS", # could be "Nelder-Mead"
                     control=list(trace=FALSE,maxit=200),hessian=TRUE)
  theta <- res.optim$par
}

Finally, let’s compute the standard deviation of the parameter estimates, using Eq. (3.4):

eps <- .0001
g0 <- f_aux(theta)$g
D <- NULL
for(i in 1:length(theta)){
  theta.i <- theta
  theta.i[i] <- theta.i[i] + eps
  gi <- f_aux(theta.i)$g
  D <- cbind(D,(gi-g0)/eps)
}
V <- 1/T * solve(t(D) %*% W %*% D)
std.dev <- sqrt(diag(V));t.stud <- theta/std.dev
cbind(theta,std.dev,t.stud)

##            theta    std.dev     t.stud
## [1,]  -0.7180716  0.4646617 -1.5453642
## [2,] -11.2042452 17.1039449 -0.6550679

The Hansen statistic can be used to test the model (see Eq. (3.5)). If the model is correct, we have: \[ T g(\underline{y_T};{\boldsymbol\theta})'\, S^{-1} \, g(\underline{y_T};{\boldsymbol\theta}) \sim \,i.i.d.\,\chi^2(J - K), \] where \(J\) is the number of moment constraints (\(n_z \times n_r\) here) and \(K\) is the number of estimated parameters (\(=n_F\) here).

g <- f_aux(theta)$g
Hansen_stat <- T * t(g) %*% W %*% g
pvalue <- pchisq(q = Hansen_stat,df = n_R*n_z - n_F)
pvalue

##           [,1]
## [1,] 0.8789782

3.2 Maximum Likelihood Estimation

3.2.1 Intuition

Intuitively, the Maximum Likelihood Estimation (MLE) consists in looking for the value of \({\boldsymbol\theta}\) that is such that the probability of having observed \(\mathbf{y}\) (the sample at hand) is the highest possible.

To set an example, assume that the time periods between the arrivals of two customers in a shop, denoted by \(y_i\), are i.i.d. and follow an exponential distribution, i.e. \(y_i \sim \,i.i.d.\, \mathcal{E}(\lambda)\). You have observed these arrivals for some time, thereby constituting a sample \(\mathbf{y}=\{y_1,\dots,y_n\}\). You want to estimate \(\lambda\) (i.e. in that case, the vector of parameters is simply \({\boldsymbol\theta} = \lambda\)).

The density of \(Y\) (one observation) is \(f(y;\lambda) = \dfrac{1}{\lambda}\exp(-y/\lambda)\). Fig. 3.1 represents such density functions for different values of \(\lambda\).

Your 200 observations are reported at the bottom of Fig. 3.1 (red bars). You build the histogram and display it on the same chart.

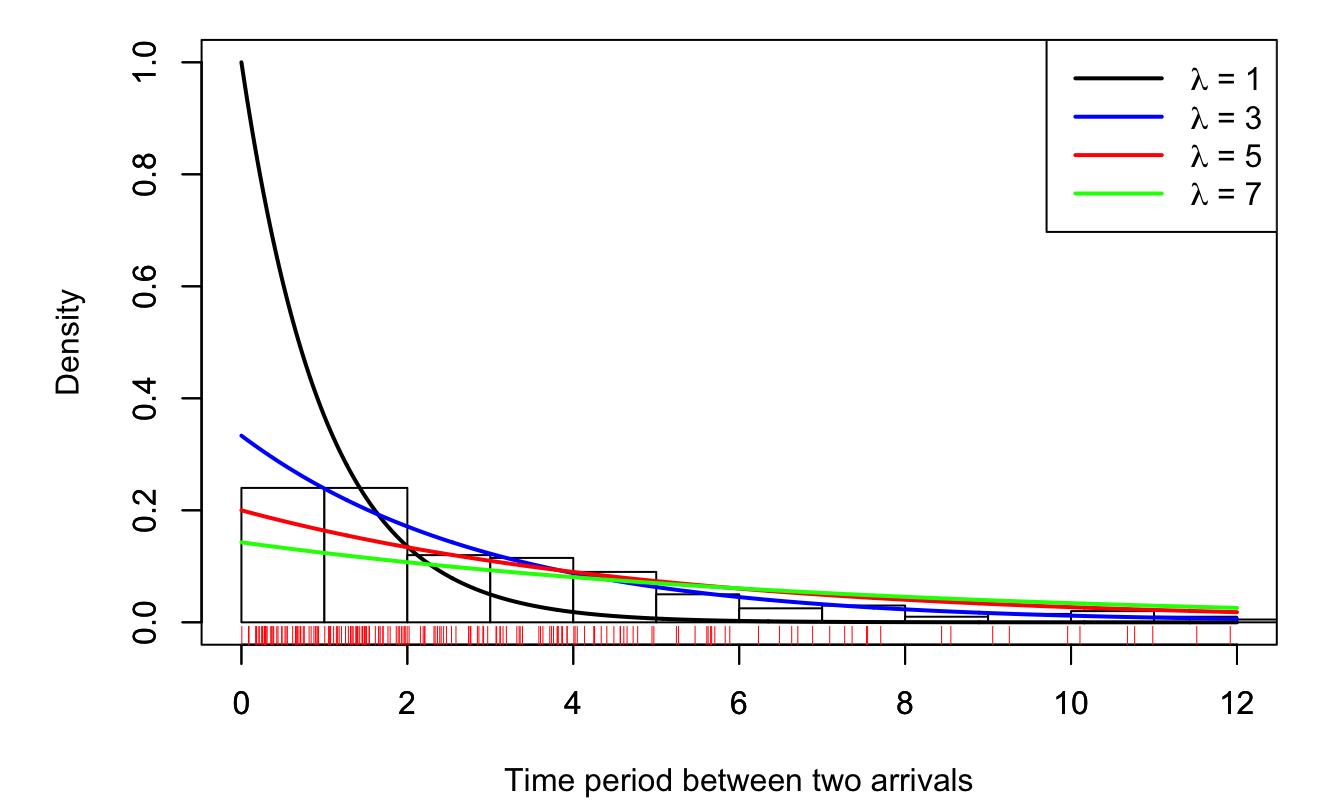
Figure 3.1: The red ticks, at the bottom, indicate observations (there are 200 of them). The historgram is based on these 200 observations

What is your estimate of \(\lambda\)? Intuitively, one is led to take the \(\lambda\) for which the (theoretical) distribution is the closest to the histogram (that can be seen as an “empirical distribution”). This approach is consistent with the idea of picking the \(\lambda\) for which the probability of observing the values included in \(\mathbf{y}\) is the highest.

Let us be more formal. Assume that you have only four observations: \(y_1=1.1\), \(y_2=2.2\), \(y_3=0.7\) and \(y_4=5.0\). What was the probability of jointly observing:

• \(1.1-\varepsilon \le Y_1 < 1.1+\varepsilon\),
• \(2.2-\varepsilon \le Y_2 < 2.2+\varepsilon\),
• \(0.7-\varepsilon \le Y_3 < 0.7+\varepsilon\), and
• \(5.0-\varepsilon \le Y_4 < 5.0+\varepsilon\)?

Because the \(y_i\)’s are i.i.d., this probability is \(\prod_{i=1}^4(2\varepsilon f(y_i,\lambda))\). The next plot shows the probability (divided by \(16\varepsilon^4\), which does not depend on \(\lambda\)) as a function of \(\lambda\).

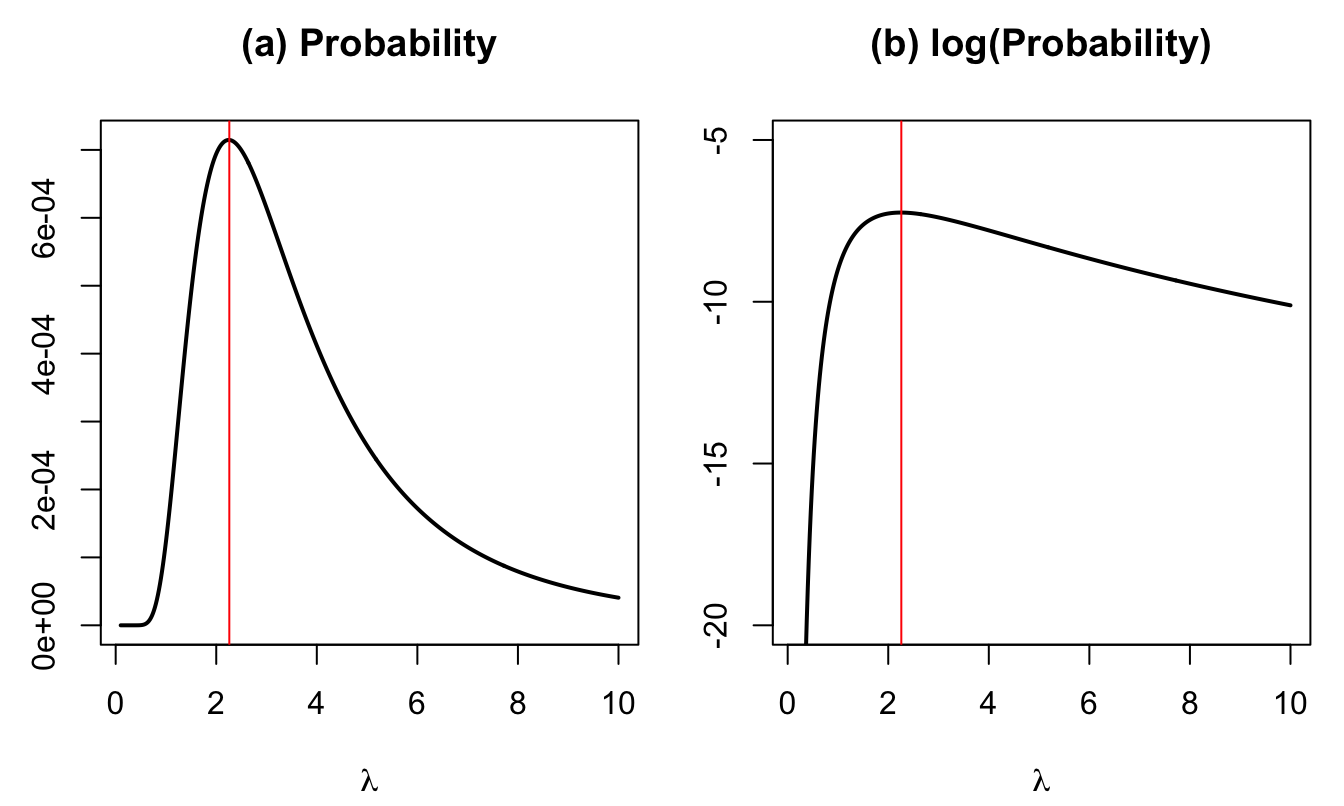
Figure 3.2: Proba. that \(y_i-\varepsilon \le Y_i < y_i+\varepsilon\), \(i \in \{1,2,3,4\}\). The vertical red line indicates the maximum of the function.

The value of \(\lambda\) that maximizes the probability is 2.26.

Let us come back to the example with 200 observations:

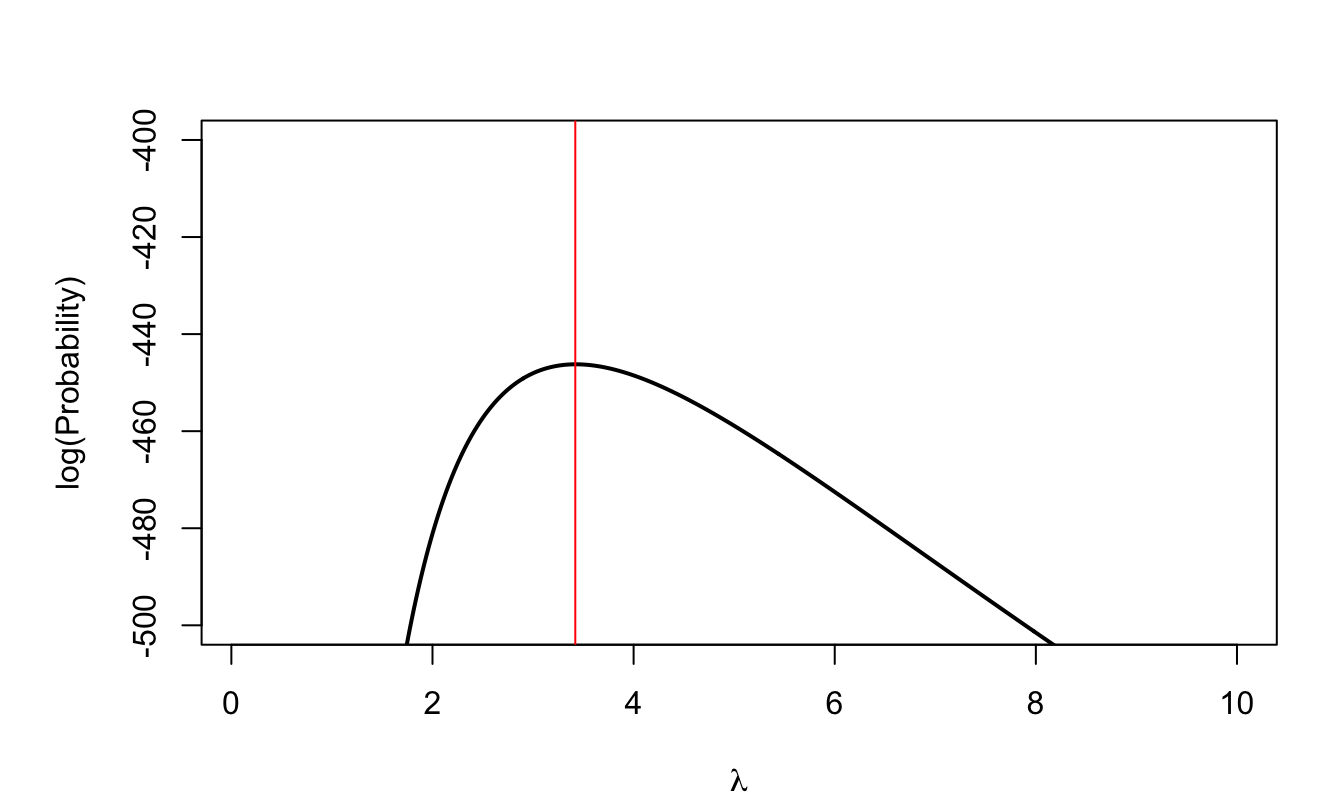
Figure 3.3: Log-likelihood function associated with the 200 i.i.d. observations. The vertical red line indicates the maximum of the function.

In that case, the value of \(\lambda\) that maxmimizes the probability is 3.42.

3.2.2 Definition and properties

\(f(y;\boldsymbol\theta)\) denotes the probability density function (p.d.f.) of a random variable \(Y\) which depends on a set of parameters \(\boldsymbol\theta\). The density of \(n\) independent and identically distributed (i.i.d.) observations of \(Y\) is given by: \[ f(\mathbf{y};\boldsymbol\theta) = \prod_{i=1}^n f(y_i;\boldsymbol\theta), \] where \(\mathbf{y}\) denotes the vector of observations; \(\mathbf{y} = \{y_1,\dots,y_n\}\).

Definition 3.2 (Likelihood function) The likelihood function is: \[ \mathcal{L}: \boldsymbol\theta \rightarrow \mathcal{L}(\boldsymbol\theta;\mathbf{y})=f(\mathbf{y};\boldsymbol\theta)=f(y_1,\dots,y_n;\boldsymbol\theta). \]

We often work with \(\log \mathcal{L}\), the log-likelihood function.

Example 3.1 (Gaussian distribution) If \(y_i \sim \mathcal{N}(\mu,\sigma^2)\), then \[ \log \mathcal{L}(\boldsymbol\theta;\mathbf{y}) = - \frac{1}{2}\sum_{i=1}^n\left( \log \sigma^2 + \log 2\pi + \frac{(y_i-\mu)^2}{\sigma^2} \right). \]

Definition 3.3 (Score) The score \(S(y;\boldsymbol\theta)\) is given by \(\frac{\partial \log f(y;\boldsymbol\theta)}{\partial \boldsymbol\theta}\).

If \(y_i \sim \mathcal{N}(\mu,\sigma^2)\) (Example 3.1), then \[ \frac{\partial \log f(y;\boldsymbol\theta)}{\partial \boldsymbol\theta} = \left[\begin{array}{c} \dfrac{\partial \log f(y;\boldsymbol\theta)}{\partial \mu}\\ \dfrac{\partial \log f(y;\boldsymbol\theta)}{\partial \sigma^2} \end{array}\right] = \left[\begin{array}{c} \dfrac{y-\mu}{\sigma^2}\\ \frac{1}{2\sigma^2}\left(\frac{(y-\mu)^2}{\sigma^2}-1\right) \end{array}\right]. \]

Proposition 3.1 (Score expectation) The expectation of the score is zero.

Proof. We have: \[\begin{eqnarray*} \mathbb{E}\left(\frac{\partial \log f(Y;\boldsymbol\theta)}{\partial \boldsymbol\theta}\right) &=& \int \frac{\partial \log f(y;\boldsymbol\theta)}{\partial \boldsymbol\theta} f(y;\boldsymbol\theta) dy \\ &=& \int \frac{\partial f(y;\boldsymbol\theta)/\partial \boldsymbol\theta}{f(y;\boldsymbol\theta)} f(y;\boldsymbol\theta) dy = \frac{\partial}{\partial \boldsymbol\theta} \int f(y;\boldsymbol\theta) dy\\ &=&\partial 1 /\partial \boldsymbol\theta = 0, \end{eqnarray*}\] which gives the result.

Definition 3.4 (Fisher information matrix) The information matrix is (minus) the the expectation of the second derivatives of the log-likelihood function: \[ \mathcal{I}_Y(\boldsymbol\theta) = - \mathbb{E} \left( \frac{\partial^2 \log f(Y;\boldsymbol\theta)}{\partial \boldsymbol\theta \partial \boldsymbol\theta'} \right). \]

Proposition 3.2 We have \[ \mathcal{I}_Y(\boldsymbol\theta) = \mathbb{E} \left[ \left( \frac{\partial \log f(Y;\boldsymbol\theta)}{\partial \boldsymbol\theta} \right) \left( \frac{\partial \log f(Y;\boldsymbol\theta)}{\partial \boldsymbol\theta} \right)' \right] = \mathbb{V}ar[S(Y;\boldsymbol\theta)]. \]

Proof. We have \(\frac{\partial^2 \log f(Y;\boldsymbol\theta)}{\partial \boldsymbol\theta \partial \boldsymbol\theta'} = \frac{\partial^2 f(Y;\boldsymbol\theta)}{\partial \boldsymbol\theta \partial \boldsymbol\theta'}\frac{1}{f(Y;\boldsymbol\theta)} - \frac{\partial \log f(Y;\boldsymbol\theta)}{\partial \boldsymbol\theta}\frac{\partial \log f(Y;\boldsymbol\theta)}{\partial \boldsymbol\theta'}\). The expectation of the first right-hand side term is \(\partial^2 1 /(\partial \boldsymbol\theta \partial \boldsymbol\theta') = \mathbf{0}\), which gives the result.

Example 3.2 If \(y_i \sim\,i.i.d.\, \mathcal{N}(\mu,\sigma^2)\), let \(\boldsymbol\theta = [\mu,\sigma^2]'\) then \[ \frac{\partial \log f(y;\boldsymbol\theta)}{\partial \boldsymbol\theta} = \left[\frac{y-\mu}{\sigma^2} \quad \frac{1}{2\sigma^2}\left(\frac{(y-\mu)^2}{\sigma^2}-1\right) \right]', \] and \[ \mathcal{I}_Y(\boldsymbol\theta) = \mathbb{E}\left( \frac{1}{\sigma^4} \left[ \begin{array}{cc} \sigma^2&y-\mu\\ y-\mu & \frac{(y-\mu)^2}{\sigma^2}-\frac{1}{2} \end{array}\right] \right)= \left[ \begin{array}{cc} 1/\sigma^2&0\\ 0 & 1/(2\sigma^4) \end{array}\right]. \]

Proposition 3.3 (Additive property of the Information matrix) The information matrix resulting from two independent experiments is the sum of the information matrices: \[ \mathcal{I}_{X,Y}(\boldsymbol\theta) = \mathcal{I}_X(\boldsymbol\theta) + \mathcal{I}_Y(\boldsymbol\theta). \]

Proof. Directly deduced from the definition of the information matrix (Def. 3.4), using that the epxectation of a product of independent variables is the product of the expectations.

Theorem 3.1 (Frechet-Darmois-Cramer-Rao bound) Consider an unbiased estimator of \(\boldsymbol\theta\) denoted by \(\hat{\boldsymbol\theta}(Y)\). The variance of the random variable \(\boldsymbol\omega'\hat{\boldsymbol\theta}\) (which is a linear combination of the components of \(\hat{\boldsymbol\theta}\)) is larger than: \[ (\boldsymbol\omega'\boldsymbol\omega)^2/(\boldsymbol\omega' \mathcal{I}_Y(\boldsymbol\theta) \boldsymbol\omega). \]

Proof. The Cauchy-Schwarz inequality implies that \(\sqrt{\mathbb{V}ar(\boldsymbol\omega'\hat{\boldsymbol\theta}(Y))\mathbb{V}ar(\boldsymbol\omega'S(Y;\boldsymbol\theta))} \ge |\boldsymbol\omega'\mathbb{C}ov[\hat{\boldsymbol\theta}(Y),S(Y;\boldsymbol\theta)]\boldsymbol\omega |\). Now, \(\mathbb{C}ov[\hat{\boldsymbol\theta}(Y),S(Y;\boldsymbol\theta)] = \int_y \hat{\boldsymbol\theta}(y) \frac{\partial \log f(y;\boldsymbol\theta)}{\partial \boldsymbol\theta} f(y;\boldsymbol\theta)dy = \frac{\partial}{\partial \boldsymbol\theta}\int_y \hat{\boldsymbol\theta}(y) f(y;\boldsymbol\theta)dy = \mathbf{I}\) because \(\hat{\boldsymbol\theta}\) is unbiased. Therefore \(\mathbb{V}ar(\boldsymbol\omega'\hat{\boldsymbol\theta}(Y)) \ge \mathbb{V}ar(\boldsymbol\omega'S(Y;\boldsymbol\theta))^{-1} (\boldsymbol\omega'\boldsymbol\omega)^2\). Prop. 3.2 leads to the result.

Definition 3.5 (Identifiability) The vector of parameters \(\boldsymbol\theta\) is identifiable if, for any other vector \(\boldsymbol\theta^*\): \[ \boldsymbol\theta^* \ne \boldsymbol\theta \Rightarrow \mathcal{L}(\boldsymbol\theta^*;\mathbf{y}) \ne \mathcal{L}(\boldsymbol\theta;\mathbf{y}). \]

Definition 3.6 (Maximum Likelihood Estimator (MLE)) The maximum likelihood estimator (MLE) is the vector \(\boldsymbol\theta\) that maximizes the likelihood function. Formally: \[\begin{equation} \boldsymbol\theta_{MLE} = \arg \max_{\boldsymbol\theta} \mathcal{L}(\boldsymbol\theta;\mathbf{y}) = \arg \max_{\boldsymbol\theta} \log \mathcal{L}(\boldsymbol\theta;\mathbf{y}).\tag{3.8} \end{equation}\]

Definition 3.7 (Likelihood equation) A necessary condition for maximizing the likelihood function (under regularity assumption, see Hypotheses 3.1) is: \[\begin{equation} \dfrac{\partial \log \mathcal{L}(\boldsymbol\theta;\mathbf{y})}{\partial \boldsymbol\theta} = \mathbf{0}. \end{equation}\]

Hypothesis 3.1 (Regularity assumptions) We have:

1. \(\boldsymbol\theta \in \Theta\) where \(\Theta\) is compact.
2. \(\boldsymbol\theta_0\) is identified.
3. The log-likelihood function is continuous in \(\boldsymbol\theta\).
4. \(\mathbb{E}_{\boldsymbol\theta_0}(\log f(Y;\boldsymbol\theta))\) exists.
5. The log-likelihood function is such that \((1/n)\log\mathcal{L}(\boldsymbol\theta;\mathbf{y})\) converges almost surely to \(\mathbb{E}_{\boldsymbol\theta_0}(\log f(Y;\boldsymbol\theta))\), uniformly in \(\boldsymbol\theta \in \Theta\).
6. The log-likelihood function is twice continuously differentiable in an open neighborood of \(\boldsymbol\theta_0\).
7. The matrix \(\mathbf{I}(\boldsymbol\theta_0) = - \mathbb{E}_0 \left( \frac{\partial^2 \log \mathcal{L}(\boldsymbol\theta;\mathbf{y})}{\partial \boldsymbol\theta \partial \boldsymbol\theta'}\right)\) —the Fisher Information matrix— exists and is nonsingular.

Proposition 3.4 (Properties of MLE) Under regularity conditions (Assumptions 3.1), the MLE is:

1. Consistent: \(\mbox{plim}\; \boldsymbol\theta_{MLE} = {\boldsymbol\theta}_0\) (\({\boldsymbol\theta}_0\) is the true vector of parameters).
2. Asymptotically normal: \[\begin{equation} \boxed{\sqrt{n}(\boldsymbol\theta_{MLE} - \boldsymbol\theta_{0}) \overset{d}{\rightarrow} \mathcal{N}(0,\mathcal{I}_Y(\boldsymbol\theta_0)^{-1}).} \tag{3.9} \end{equation}\]
3. Asymptotically efficient: \(\boldsymbol\theta_{MLE}\) is asymptotically efficient and achieves the Freechet-Darmois-Cramer-Rao lower bound for consistent estimators.
4. Invariant: The MLE of \(g(\boldsymbol\theta_0)\) is \(g(\boldsymbol\theta_{MLE})\) if \(g\) is a continuous and continuously differentiable function.

Proof. See Appendix 8.4.

Since \(\mathcal{I}_Y(\boldsymbol\theta_0)=\frac{1}{n}\mathbf{I}(\boldsymbol\theta_0)\), the asymptotic covariance matrix of the MLE is \([\mathbf{I}(\boldsymbol\theta_0)]^{-1}\), that is: \[ [\mathbf{I}(\boldsymbol\theta_0)]^{-1} = \left[- \mathbb{E}_0 \left( \frac{\partial^2 \log \mathcal{L}(\boldsymbol\theta;\mathbf{y})}{\partial \boldsymbol\theta \partial \boldsymbol\theta'}\right) \right]^{-1}. \] A direct (analytical) evaluation of this expectation is often out of reach. It can however be estimated by, either: \[\begin{eqnarray} \hat{\mathbf{I}}_1^{-1} &=& \left( - \frac{\partial^2 \log \mathcal{L}({\boldsymbol\theta_{MLE}};\mathbf{y})}{\partial {\boldsymbol\theta} \partial {\boldsymbol\theta}'}\right)^{-1}, \tag{3.10}\\ \hat{\mathbf{I}}_2^{-1} &=& \left( \sum_{i=1}^n \frac{\partial \log \mathcal{L}({\boldsymbol\theta_{MLE}};y_i)}{\partial {\boldsymbol\theta}} \frac{\partial \log \mathcal{L}({\boldsymbol\theta_{MLE}};y_i)}{\partial {\boldsymbol\theta'}} \right)^{-1}. \tag{3.11} \end{eqnarray}\]

Asymptotically, we have \((\hat{\mathbf{I}}_1^{-1})\hat{\mathbf{I}}_2=Id\), that is, the two formulas provide the same result.

In case of (suspected) misspecification, one can use the so-called sandwich estimator of the covariance matrix.⁸ This covariance matrix is given by: \[\begin{equation} \hat{\mathbf{I}}_3^{-1} = \hat{\mathbf{I}}_2^{-1} \hat{\mathbf{I}}_1 \hat{\mathbf{I}}_2^{-1}.\tag{3.12} \end{equation}\]

3.2.3 To sum up – MLE in practice

To implement MLE, we need:

• A parametric model (depending on the vector of parameters \(\boldsymbol\theta\) whose “true” value is \(\boldsymbol\theta_0\)) is specified.
• i.i.d. sources of randomness are identified.
• The density associated to one observation \(y_i\) is computed analytically (as a function of \(\boldsymbol\theta\)): \(f(y;\boldsymbol\theta)\).
• The log-likelihood is \(\log \mathcal{L}(\boldsymbol\theta;\mathbf{y}) = \sum_i \log f(y_i;\boldsymbol\theta)\).
• The MLE estimator results from the optimization problem (this is Eq. (3.8)): \[\begin{equation} \boldsymbol\theta_{MLE} = \arg \max_{\boldsymbol\theta} \log \mathcal{L}(\boldsymbol\theta;\mathbf{y}). \end{equation}\]
• We have: \(\boldsymbol\theta_{MLE} \sim \mathcal{N}({\boldsymbol\theta}_0,\mathbf{I}(\boldsymbol\theta_0)^{-1})\), where \(\mathbf{I}(\boldsymbol\theta_0)^{-1}\) is estimated by means of Eq. (3.10), Eq. (3.11), or Eq. (3.12). Most of the time, this computation is numerical.

3.2.4 Example: MLE estimation of a mixture of Gaussian distribution

Consider the returns of the Swiss Market Index (SMI). Assume that these returns are independently drawn from a mixture of Gaussian distributions. The p.d.f. \(f(x;\boldsymbol\theta)\), with \(\boldsymbol\theta = [\mu_1,\sigma_1,\mu_2,\sigma_2,p]'\), is given by: \[ p \frac{1}{\sqrt{2\pi\sigma_1^2}}\exp\left(-\frac{(x - \mu_1)^2}{2\sigma_1^2}\right) + (1-p)\frac{1}{\sqrt{2\pi\sigma_2^2}}\exp\left(-\frac{(x - \mu_2)^2}{2\sigma_2^2}\right). \] (See p.d.f. of mixtures of Gaussian distributions.)

library(AEC);data(smi)
T <- dim(smi)[1]
h <- 5 # holding period (one week)
smi$r <- c(rep(NaN,h),
           100*c(log(smi$Close[(1+h):T]/smi$Close[1:(T-h)])))
indic.dates <- seq(1,T,by=5)  # weekly returns
smi <- smi[indic.dates,]
smi <- smi[complete.cases(smi),]
par(mfrow=c(1,1));par(plt=c(.15,.95,.1,.95))
plot(smi$Date,smi$r,type="l",xlab="",ylab="in percent")
abline(h=0,col="blue")
abline(h=mean(smi$r,na.rm = TRUE)+2*sd(smi$r,na.rm = TRUE),lty=3,col="blue")
abline(h=mean(smi$r,na.rm = TRUE)-2*sd(smi$r,na.rm = TRUE),lty=3,col="blue")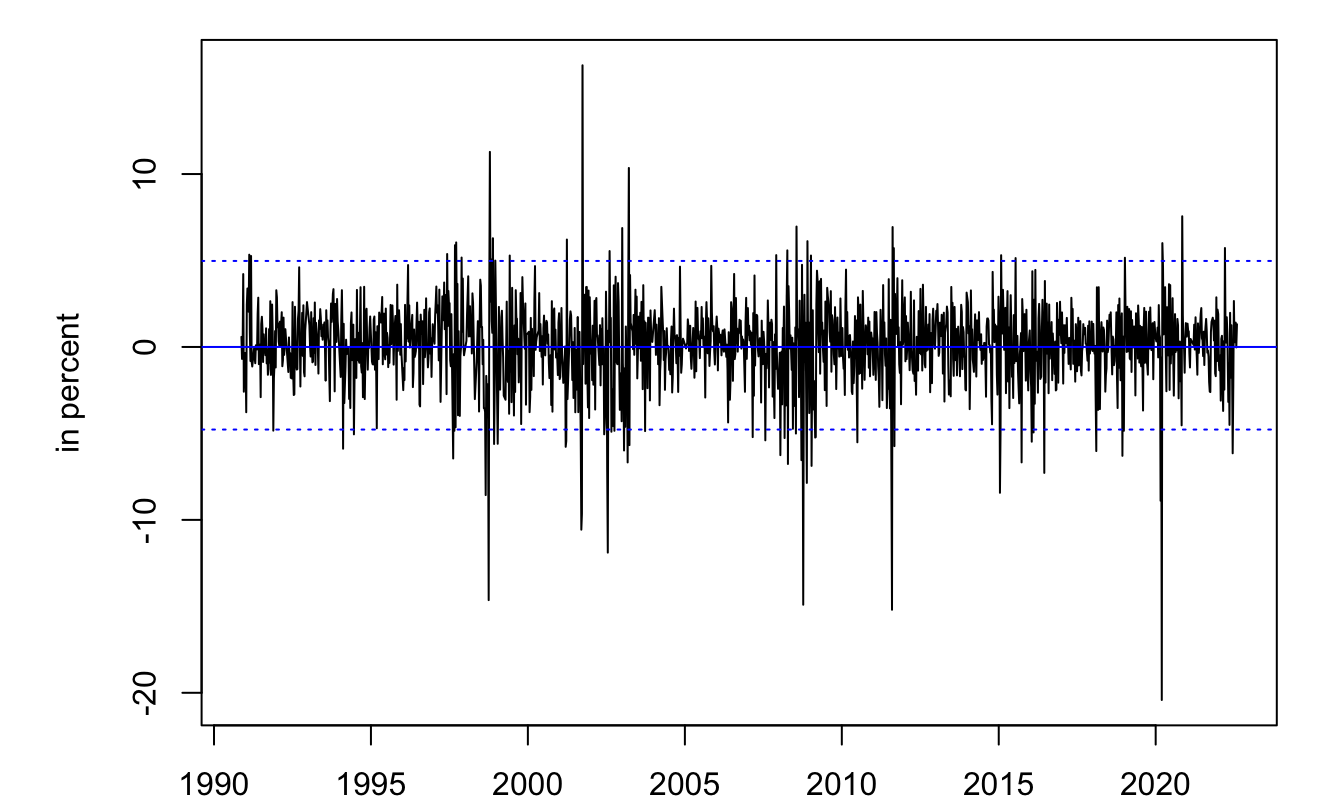

Figure 3.4: Time series of SMI weekly returns (source: Yahoo Finance).

Build the log-likelihood function (fucntion log.f), and use the numerical BFGS algorithm to maximize it (using the optim wrapper):

f <- function(theta,y){ # Likelihood function
  mu.1 <- theta[1]; mu.2 <- theta[2]
  sigma.1 <- theta[3]; sigma.2 <- theta[4]
  p <- exp(theta[5])/(1+exp(theta[5]))
  res <- p*1/sqrt(2*pi*sigma.1^2)*exp(-(y-mu.1)^2/(2*sigma.1^2)) +
    (1-p)*1/sqrt(2*pi*sigma.2^2)*exp(-(y-mu.2)^2/(2*sigma.2^2))
  return(res)
}
log.f <- function(theta,y){ #log-Likelihood function
  return(-sum(log(f(theta,y))))
}
res.optim <- optim(c(0,0,0.5,1.5,.5),
                   log.f,
                   y=smi$r,
                   method="BFGS", # could be "Nelder-Mead"
                   control=list(trace=FALSE,maxit=100),hessian=TRUE)
theta <- res.optim$par
theta

## [1]  0.3012379 -1.3167476  1.7715072  4.8197596  1.9454889

Next, compute estimates of the covariance matrix of the MLE (using Eqs. (3.10), (3.11), and (3.12)), and compare the three sets of resulting standard deviations for the five estimated paramters:

# Hessian approach:
I.1 <- solve(res.optim$hessian)
# Outer-product of gradient approach:
log.f.0 <- log(f(theta,smi$r))
epsilon <- .00000001
d.log.f <- NULL
for(i in 1:length(theta)){
  theta.i <- theta
  theta.i[i] <- theta.i[i] + epsilon
  log.f.i <- log(f(theta.i,smi$r))
  d.log.f <- cbind(d.log.f,
                   (log.f.i - log.f.0)/epsilon)
}
I.2 <- solve(t(d.log.f) %*% d.log.f)
# Misspecification-robust approach (sandwich formula):
I.3 <- I.1 %*% solve(I.2) %*% I.1
cbind(diag(I.1),diag(I.2),diag(I.3))

##             [,1]        [,2]       [,3]
## [1,] 0.003683422 0.003199481 0.00586160
## [2,] 0.226892824 0.194283391 0.38653389
## [3,] 0.005764271 0.002769579 0.01712255
## [4,] 0.194081311 0.047466419 0.83130838
## [5,] 0.092114437 0.040366005 0.31347858

According to the first (respectively third) type of estimate for the covariance matrix, a 95% confidence interval for \(\mu_1\) is [0.182, 0.42] (resp. [0.151, 0.451]).

Note that we have not directly estimated parameter \(p\) but \(\nu = \log(p/(1-p))\) (in such a way that \(p = \exp(\nu)/(1+\exp(\nu))\)). In order to get an estimate of the standard deviation of our esitmate of \(p\), we can implement the Delta method. This method is based on the fact that, for a function \(g\) that is continuous in the neighborhood of \(\boldsymbol\theta_0\) and for large \(n\), we have: \[\begin{equation} \mathbb{V}ar(g(\hat{\boldsymbol\theta}_n)) \approx \frac{\partial g(\hat{\boldsymbol\theta}_n)}{\partial \boldsymbol\theta'}\mathbb{V}ar(\hat{\boldsymbol\theta}_n)\frac{\partial g(\hat{\boldsymbol\theta}_n)'}{\partial \boldsymbol\theta}.\tag{3.13} \end{equation}\]

g <- function(theta){
  mu.1 <- theta[1]; mu.2 <- theta[2]
  sigma.1 <- theta[3]; sigma.2 <- theta[4]
  p <- exp(theta[5])/(1+exp(theta[5]))
  return(c(mu.1,mu.2,sigma.1,sigma.2,p))
}
# Computation of g's gradient around estimated theta:
eps <- .00001
g.theta <- g(theta)
g.gradient <- NULL
for(i in 1:5){
  theta.perturb <- theta
  theta.perturb[i] <- theta[i] + eps
  g.gradient <- cbind(g.gradient,(g(theta.perturb)-g.theta)/eps)
}
Var <- g.gradient %*% I.3 %*% t(g.gradient)
stdv.g.theta <- sqrt(diag(Var))
stdv.theta <- sqrt(diag(I.3))
cbind(theta,stdv.theta,g.theta,stdv.g.theta)

##           theta stdv.theta    g.theta stdv.g.theta
## [1,]  0.3012379 0.07656108  0.3012379   0.07656108
## [2,] -1.3167476 0.62171850 -1.3167476   0.62171850
## [3,]  1.7715072 0.13085316  1.7715072   0.13085316
## [4,]  4.8197596 0.91176114  4.8197596   0.91176114
## [5,]  1.9454889 0.55989158  0.8749539   0.06125726

The previous results show that the MLE estimate of \(p\) is 0.8749539, and its standard deviation is approximately equal to 0.0612573.

To finish with, let us draw the estimated parametric p.d.f. (the mixture of Gaussian distribution), and compare it to a non-parametric (kernel-based) estimate of this p.d.f. (using function density):

x <- seq(-5,5,by=.01)
par(plt=c(.1,.95,.1,.95))
plot(x,f(theta,x),type="l",lwd=2,xlab="returns, in percent",ylab="",
     ylim=c(0,1.4*max(f(theta,x))))
lines(density(smi$r),type="l",lwd=2,lty=3)
lines(x,dnorm(x,mean=mean(smi$r),sd = sd(smi$r)),col="red",lty=2,lwd=2)
rug(smi$r,col="blue")
legend("topleft",
       c("Kernel estimate (non-parametric)",
         "Estimated mixture of Gaussian distr. (MLE, parametric)",
         "Normal distribution"),
       lty=c(3,1,2),lwd=c(2), # line width
       col=c("black","black","red"),pt.bg=c(1),pt.cex = c(1),
       bg="white",seg.len = 4)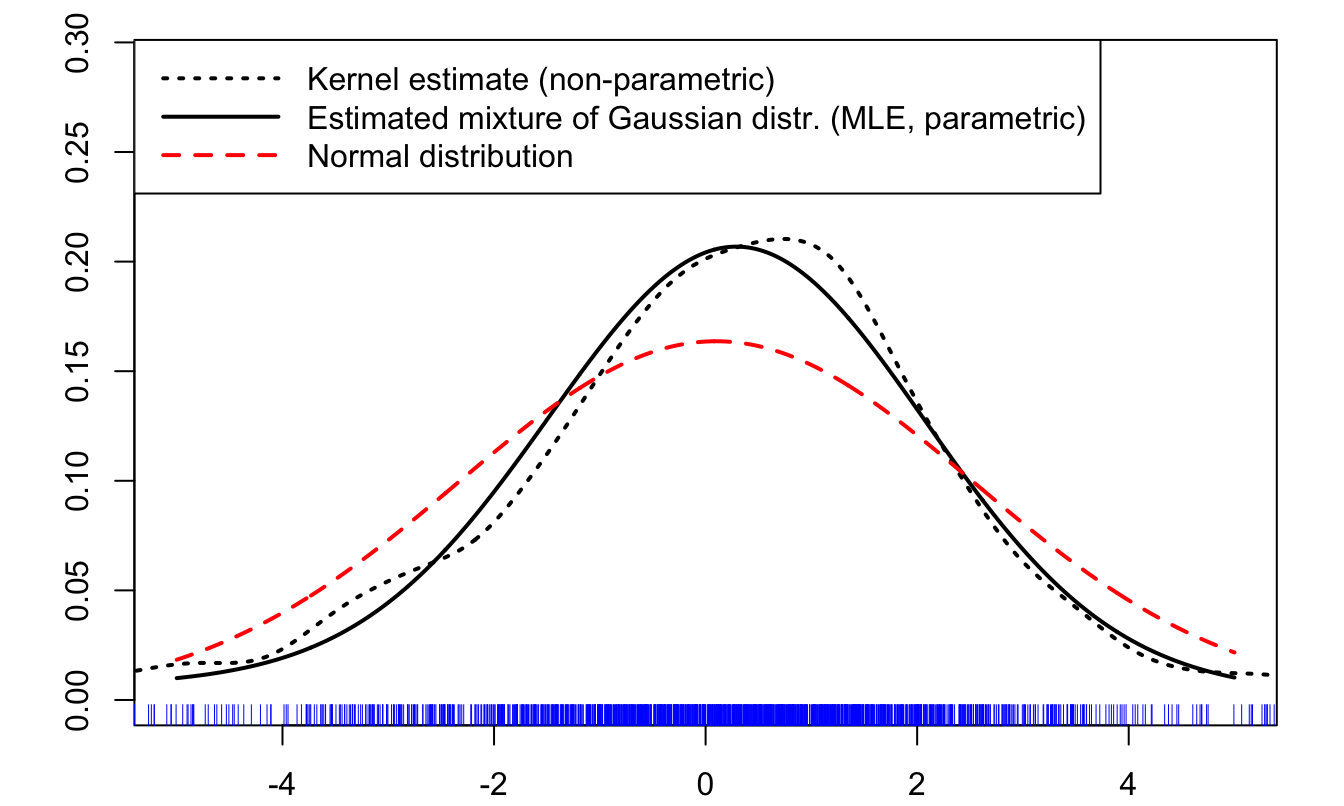

Figure 3.5: Comparison of different estimates of the distribution of returns.

3.2.5 Test procedures

Suppose we want to test the following parameter restrictions: \[\begin{equation} \boxed{H_0: \underbrace{h(\boldsymbol\theta)}_{r \times 1}=0.} \end{equation}\]

In the context of MLE, three tests are largely used:

• Likelihood Ratio (LR) test,
• Wald (W) test,
• Lagrange Multiplier (LM) test.

Here is the rationale behind these three tests:⁹

• LR: If \(h(\boldsymbol\theta)=0\), then imposing this restriction during the estimation (restricted estimator) should not result in a large decrease in the likelihood function (w.r.t the unrestricted estimation).
• Wald: If \(h(\boldsymbol\theta)=0\), then \(h(\hat{\boldsymbol\theta})\) should not be far from \(0\) (even if these restrictions are not imposed during the MLE).
• LM: If \(h(\boldsymbol\theta)=0\), then the gradient of the likelihood function should be small when evaluated at the restricted estimator.

In terms of implementation, while the LR necessitates to estimate both restricted and unrestricted models, the Wald test requires the estimation of the unrestricted model only, and the LM tests requires the estimation of the restricted model only.

As shown below, the three test statistics associated with these three tests coincide asymptotically. (Therefore, they naturally have the same asymptotic distribution, that are \(\chi^2\).)

Proposition 3.5 (Asymptotic distribution of the Wald statistic) Under regularity conditions (Assumptions 3.1) and under \(H_0: h(\boldsymbol\theta)=0\), the Wald statistic, defined by: \[ \boxed{\xi^W = h(\hat{\boldsymbol\theta})' \mathbb{V}ar[h(\hat{\boldsymbol\theta})]^{-1} h(\hat{\boldsymbol\theta}),} \] where \[\begin{equation} \mathbb{V}ar[h(\hat{\boldsymbol\theta})] = \left(\frac{\partial h(\hat{\boldsymbol\theta})}{\partial \boldsymbol\theta'} \right) \mathbb{V}ar[\hat{\boldsymbol\theta}] \left(\frac{\partial h(\hat{\boldsymbol\theta})'}{\partial \boldsymbol\theta} \right),\tag{3.14} \end{equation}\] is asymptotically \(\chi^2(r)\), where the number of degrees of freedom \(r\) corresponds to the dimension of \(h(\boldsymbol\theta)\). (Note that Eq. (3.14) is the same as the one used in the Delta method, see Eq. (3.13).)

The Wald test, defined by the critical region \[ \{\xi^W \ge \chi^2_{1-\alpha}(r)\}, \] where \(\chi^2_{1-\alpha}(r)\) denotes the quantile of level \(1-\alpha\) of the \(\chi^2(r)\) distribution, has asymptotic level \(\alpha\) and is consistent.¹⁰

Proof. See Appendix 8.4.

In practice, in Eq. (3.14), \(\mathbb{V}ar[\hat{\boldsymbol\theta}]\) is replaced by an estimate given, e.g., by Eq. (3.10), Eq. (3.11), or Eq. (3.12).

Proposition 3.6 (Asymptotic distribution of the LM test statistic) Under regularity conditions (Assumptions 3.1) and under \(H_0: h(\boldsymbol\theta)=0\), the LM statistic \[\begin{equation} \boxed{\xi^{LM} = \left(\left.\frac{\partial \log \mathcal{L}(\boldsymbol\theta)}{\partial \boldsymbol\theta'}\right|_{\boldsymbol\theta = \hat{\boldsymbol\theta}^0} \right) [\mathbf{I}(\hat{\boldsymbol\theta}^0)]^{-1} \left(\left.\frac{\partial \log \mathcal{L}(\boldsymbol\theta)}{\partial \boldsymbol\theta }\right|_{\boldsymbol\theta = \hat{\boldsymbol\theta}^0} \right),} \tag{3.15} \end{equation}\] (where \(\hat{\boldsymbol\theta}^0\) is the restricted MLE estimator) is \(\chi^2(r)\).

The test defined by the critical region: \[ \{\xi^{LM} \ge \chi^2_{1-\alpha}(r)\} \] has asymptotic level \(\alpha\) and is consistent (see Defs. 8.7 and 8.8). This test is called Score or Lagrange Multiplier (LM) test.

Proof. See Appendix 8.4.

Definition 3.8 (Likelihood Ratio test statistics) The likelihood ratio associated to a restriction of the form \(H_0: h({\boldsymbol\theta})=0\) is given by: \[ LR = \frac{\mathcal{L}_R(\boldsymbol\theta;\mathbf{y})}{\mathcal{L}_U(\boldsymbol\theta;\mathbf{y})} \quad (\in [0,1]), \] where \(\mathcal{L}_R\) (respectively \(\mathcal{L}_U\)) is the likelihood function that imposes (resp. that does not impose) the restriction. The likelihood ratio test statistic is given by \(-2\log(LR)\), that is: \[ \boxed{\xi^{LR}= 2 (\log\mathcal{L}_U(\boldsymbol\theta;\mathbf{y})-\log\mathcal{L}_R(\boldsymbol\theta;\mathbf{y})).} \]

Proposition 3.7 (Asymptotic equivalence of LR, LM, and Wald tests) Under the null hypothesis \(H_0\), we have, asymptotically: \[ \xi^{LM} = \xi^{LR} = \xi^{W}. \]

Proof. See Appendix 8.4.

3.3 Bayesian approach

3.3.1 Introduction

An excellent introduction to Bayesian methods is proposed by Martin Haugh, 2017.

As suggested by the name of this approach, the starting point is the Bayes formula: \[ \mathbb{P}(A|B) = \frac{\mathbb{P}(A \& B)}{\mathbb{P}(B)}, \] where \(A\) and \(B\) are two “events”. For instance, \(A\) may be: parameter \(\alpha\) (conceived as something stochastic) lies in interval \([a,b]\). Assume that you are interested in the probability of occurrence of \(A\). Without any specific information (or “unconditionally”), this probability if \(\mathbb{P}(A)\). Your evaluation of this probability can only be better if you are provided with any additional form of information. Typically, if the event \(B\) tends to occur simultaneously with \(A\), then knowledge of \(B\) can be useful. The Bayes formula says how this additional information (on \(B\)) can be used to “update” the probability of event \(A\).

In our case, this intuition will work as follows: assume that you know the form of the data-generating process (DGP). That is, you know the structure of the model used to draw some stochastic data; you also know the type of distributions used to generate these data. However, you do not know the numerical values of all the parameters characterizing the DGP. Let us denote by \({\boldsymbol\theta}\) the vector of unknown parameters. While these parameters are not known exactly, assume that we have –even without having observed any data– some priors on their distribution. Then, as was the case in the example above (with \(A\) and \(B\)), the observation of data generated by the model can only reduce the uncertainty associated with \({\boldsymbol\theta}\). Loosely speaking, combining the priors and the observations of data generated by the model should result in “thinner” distributions for the components of \({\boldsymbol\theta}\). The latter distributions are called the posterior distributions.¹¹

Let us formalize this intuition. Define the prior by \(f_{\boldsymbol\theta}({\boldsymbol\theta})\) and the model realizations (the “data”) by vector \(\mathbf{y}\). The joint distribution of \((\mathbf{y},{\boldsymbol\theta})\) is given by: \[ f_{Y,{\boldsymbol\theta}}(\mathbf{y},{\boldsymbol\theta}) = f_{Y|{\boldsymbol\theta}}(\mathbf{y},{\boldsymbol\theta})f_{\boldsymbol\theta}({\boldsymbol\theta}), \] and, symmetrically, by \[ f_{Y,{\boldsymbol\theta}}(\mathbf{y},{\boldsymbol\theta}) = f_{{\boldsymbol\theta}|Y}({\boldsymbol\theta},\mathbf{y})f_Y(\mathbf{y}), \] where \(f_{{\boldsymbol\theta}|Y}(\cdot,\mathbf{y})\), the distribution of the parameters conditional on the observations, is the posterior distribution.

The last two equations imply that: \[\begin{equation} f_{{\boldsymbol\theta}|Y}({\boldsymbol\theta},\mathbf{y}) = \frac{f_{Y|{\boldsymbol\theta}}(\mathbf{y},{\boldsymbol\theta})f_{{\boldsymbol\theta}}({\boldsymbol\theta})}{f_Y(\mathbf{y})}.\tag{3.16} \end{equation}\] Note that \(f_Y\) is the marginal (or unconditional) distribution of \(\mathbf{y}\), that can be written: \[\begin{equation} f_Y(\mathbf{y}) = \int f_{Y|{\boldsymbol\theta}}(\mathbf{y},{\boldsymbol\theta})f_{\boldsymbol\theta}({\boldsymbol\theta}) d {\boldsymbol\theta}. \end{equation}\]

Eq. (3.16) is sometimes rewritten as follows: \[\begin{equation} f_{{\boldsymbol\theta}|Y}({\boldsymbol\theta},\mathbf{y}) \propto f_{{\boldsymbol\theta},Y}({\boldsymbol\theta},\mathbf{y}) := f_{Y|{\boldsymbol\theta}}(\mathbf{y},{\boldsymbol\theta})f_{\boldsymbol\theta}({\boldsymbol\theta}), \tag{3.17} \end{equation}\] where \(\propto\) means, loosely speaking, “proportional to”. In rare instances, starting from given priors, one can analytically compute the posterior distribution \(f_{\boldsymbol\theta}({\boldsymbol\theta},\mathbf{y})\). However, in most cases, this is out of reach. One then has to resort to numerical approaches to compute the posterior distribution. Monte Carlo Markov Chains (MCMC) is one of them.

According to the Bernstein-von Mises Theorem, Bayesian and MLE estimators have the same large sample properties. (In particular, the Bayesian approach also achieve the FDCR bound, see Theorem 3.1.) The intuition behind this result is that the influence of the prior diminishes with increasing sample sizes.

3.3.2 Monte-Carlo Markov Chains

MCMC techniques aim at using simulations to approach a distribution whose distribution is difficult to obtain analytically. Indeed, in some circumstances, one can draw in a distribution even if we do not know its analytical expression.

Definition 3.9 (Markov Chain) The sequence \(\{z_i\}\) is said to be a (first-order) Markovian process is it satisfies: \[ f(z_i|z_{i-1},z_{i-2},\dots) = f(z_i|z_{i-1}). \]

The Metropolis-Hastings (MH) algorithm is a specific MCMC approach that allows to generate samples of \({\boldsymbol\theta}\)’s whose distribution approximately corresponds to the posterior distribution of Eq. (3.16).

The MH algorithm is a recursive algorithm. That is, one can draw the \(i^{th}\) value of \({\boldsymbol\theta}\), denoted by \({\boldsymbol\theta}_i\), if one has already drawn \({\boldsymbol\theta}_{i-1}\). Assume we have \({\boldsymbol\theta}_{i-1}\). We obtain a value for \({\boldsymbol\theta}_i\) by implementing the following steps:

1. Draw \(\tilde{{\boldsymbol\theta}}_i\) from the conditional distribution \(Q_{\tilde{{\boldsymbol\theta}}|{\boldsymbol\theta}}(\cdot,{\boldsymbol\theta}_{i-1})\), called proposal distribution.
2. Draw \(u\) in a uniform distribution on \([0,1]\).
3. Compute \[\begin{equation} \alpha(\tilde{{\boldsymbol\theta}}_i,{\boldsymbol\theta}_{i-1}):= \min\left(\frac{f_{{\boldsymbol\theta},Y}(\tilde{{\boldsymbol\theta}}_i,\mathbf{y})}{f_{{\boldsymbol\theta},Y}({\boldsymbol\theta}_{i-1},\mathbf{y})}\times\frac{Q_{\tilde{{\boldsymbol\theta}}|{\boldsymbol\theta}}({\boldsymbol\theta}_{i-1},\tilde{{\boldsymbol\theta}}_i)}{Q_{\tilde{{\boldsymbol\theta}}|{\boldsymbol\theta}}(\tilde{{\boldsymbol\theta}}_i,{\boldsymbol\theta}_{i-1})},1\right),\tag{3.18} \end{equation}\] where \(f_{{\boldsymbol\theta},Y}\) is given in Eq. (3.17).
4. If \(u<\alpha(\tilde{{\boldsymbol\theta}}_i,{\boldsymbol\theta}_{i-1})\), then take \({\boldsymbol\theta}_i = \tilde{{\boldsymbol\theta}}_i\), otherwise we leave \({\boldsymbol\theta}_i\) equal to \({\boldsymbol\theta}_{i-1}\).

It can be shown that, the distribution of the draws converges to the posterior distribution. That is, after a sufficiently large number of iterations, the draws can be considered to be drawn from the posterior distribution.¹²

To get some insights into the algorithm, consider the case of a symmetric proposal distribution, that is: \[\begin{equation} Q_{\tilde{{\boldsymbol\theta}}|{\boldsymbol\theta}}(\tilde{{\boldsymbol\theta}}_i,{\boldsymbol\theta}_{i-1})=Q_{\tilde{{\boldsymbol\theta}}|{\boldsymbol\theta}}({\boldsymbol\theta}_{i-1},\tilde{{\boldsymbol\theta}}_i).\tag{3.19} \end{equation}\] We then have: \[\begin{equation} \alpha(\tilde{{\boldsymbol\theta}},{\boldsymbol\theta}_{i-1})= \min\left(\frac{q(\tilde{{\boldsymbol\theta}},y)}{q({\boldsymbol\theta}_{i-1},y)},1\right). \tag{3.20} \end{equation}\] Remember that, up to the marginal distribution of the data (\(f_Y(\mathbf{y})\)), \(f_{{\boldsymbol\theta},Y}(\tilde{{\boldsymbol\theta}},\mathbf{y})\) is the probability of observing \(\mathbf{y}\) conditional on having a model parameterized by \(\tilde{\boldsymbol\theta}\). Then, under Eq. (3.20), it appears that if this probability is larger for \(\tilde{\boldsymbol\theta}\) than for \({\boldsymbol\theta}_{i-1}\) (in which case \(\tilde{\boldsymbol\theta}\) seems “more consistent with the observations \(\mathbf{y}\)” than \({\boldsymbol\theta}_{i-1}\)), we accept \({\boldsymbol\theta}_i\). By contrast, if \(f_{{\boldsymbol\theta},Y}(\tilde{{\boldsymbol\theta}},\mathbf{y})<f_{{\boldsymbol\theta},Y}({\boldsymbol\theta}_{i-1},\mathbf{y})\), then we do not necessarily accept the proposed value \(\tilde{{\boldsymbol\theta}}\), especially if \(f_{{\boldsymbol\theta},Y}(\tilde{{\boldsymbol\theta}},\mathbf{y})\ll f_{{\boldsymbol\theta},Y}({\boldsymbol\theta}_{i-1},\mathbf{y})\) (in which case \(\tilde{\boldsymbol\theta}\) seems far less consistent with the observations \(\mathbf{y}\) than \({\boldsymbol\theta}_{i-1}\), and, accordingly, the acceptance probability, namely \(\alpha(\tilde{{\boldsymbol\theta}},{\boldsymbol\theta}_{i-1})\), is small).

The choice of the proposal distribution \(Q_{\tilde{\boldsymbol\theta}|{\boldsymbol\theta}}\) is crucial to get a rapid convergence of the algorithm. Looking at Eq. (3.18), it is easily seen that the optimal choice would be \(Q_{\tilde{\boldsymbol\theta}|{\boldsymbol\theta}}(\cdot,{\boldsymbol\theta}_i)=f_{{\boldsymbol\theta}|Y}(\cdot,\mathbf{y})\). In that case, we would have \(\alpha(\tilde{{\boldsymbol\theta}}_i,{\boldsymbol\theta}_{i-1})\equiv 1\) (see Eq. (3.18)). We would then accept all draws from the proposal distribution, as this distribution would directly be the posterior distribution. Of course, this situation is not realistoc as the objective of the algorithm is precisely to approximate the posterior distribution.

A common choice for \(Q\) is a multivariate normal distribution. If \({\boldsymbol\theta}\) is of dimension \(K\), we can for instance use: \[ Q(\tilde{\boldsymbol\theta},{\boldsymbol\theta})= \frac{1}{\left(\sqrt{2\pi\sigma^2}\right)^K}\exp\left(-\frac{1}{2}\sum_{j=1}^K\frac{(\tilde{\boldsymbol\theta}_j-{\boldsymbol\theta}_j)^2}{\sigma^2}\right), \] which is an example of symmetric proposal distribution (see Eq. (3.19)). Equivalently, we then have: \[ \tilde{\boldsymbol\theta} = {\boldsymbol\theta} + \varepsilon, \] where \(\varepsilon\) is a \(K\)-dimensional vector of independent zero-mean normal disturbances of variance \(\sigma^2\).¹³ One then has to determine an appropriate value for \(\sigma\). If it is too low, then \(\alpha\) will be close to 1 (as \(\tilde{{\boldsymbol\theta}}_i\) will be close to \({\boldsymbol\theta}_{i-1}\)), and we will accept very often the proposed value (\(\tilde{{\boldsymbol\theta}}_i\)). This seems to be a favourable situation. But it may not be. Indeed, it means that it will take a large number of iterations to explore the whole distribution of \({\boldsymbol\theta}\). What if \(\sigma\) is very large? In this case, it is likely that the porposed values (\(\tilde{{\boldsymbol\theta}}_i\)) will often result in poor likelihoods; The probability of acceptance will then be low and the Markov chain may be blocked at its initial value. Therefore, intermediate values of \(\sigma^2\) have to be determined. The acceptance rate (i.e., the average value of \(\alpha(\tilde{{\boldsymbol\theta}},{\boldsymbol\theta}_{i-1})\)) can be used as a guide for that. Indeed, a literature explores the optimal values for such acceptance rate (in order to obtain the best possible fit of the posterior for a minimum number of algorithm iterations). In particular, following Roberts, Gelman, and Gilks (1997), people often target acceptance rate of the order of magnitude of 20%.

It is important to note that, to implement this approach, one only has to be able to compute the joint p.d.f. \(q({\boldsymbol\theta},\mathbf{y})=f_{Y|{\boldsymbol\theta}}(\mathbf{y},{\boldsymbol\theta})f_{\boldsymbol\theta}({\boldsymbol\theta})\) (Eq. (3.17)). That is, as soon as one can evaluate the likelihood (\(f_{Y|{\boldsymbol\theta}}(\mathbf{y},{\boldsymbol\theta})\)) and the prior (\(f_{\boldsymbol\theta}({\boldsymbol\theta})\)), we can employ this methodology.

3.3.3 Example: AR(1) specification

In the following example, we employ MCMC in order to estimate the posterior distributions of the three parameters defining an AR(1) model. The specification is as follows: \[ y_t = \mu + \rho y_{t-1} + \sigma \varepsilon_{t}, \quad \varepsilon_t \sim \,i.i.d.\,\mathcal{N}(0,1). \] Hence, we have \({\boldsymbol\theta} = [\mu,\rho,\sigma]\). Let us first simulate the process on \(T\) periods:

mu <- .6; rho <- .8; sigma <- .5 # true model specification
T <- 20 # number of observations
y0 <- mu/(1-rho)
Y <- NULL
for(t in 1:T){
  if(t==1){y <- y0}
  y <- mu + rho*y + sigma * rnorm(1)
  Y <- c(Y,y)}
plot(Y,type="l",xlab="time t",ylab=expression(y[t]))

Next, let us write the likelihood function, i.e. \(f_{Y|{\boldsymbol\theta}}(\mathbf{y},{\boldsymbol\theta})\). For \(\rho\), which is expected to be between 0 and 1, we use a logistic transformation. For \(\sigma\), that is expected to be positive, we use an exponential transformation.

likelihood <- function(param,Y){
  mu  <- param[1]
  rho <- exp(param[2])/(1+exp(param[2]))
  sigma <- exp(param[3])
  MU <- mu/(1-rho)
  SIGMA2 <- sigma^2/(1-rho^2)
  L <- 1/sqrt(2*pi*SIGMA2)*exp(-(Y[1]-MU)^2/(2*SIGMA2))
  Y1 <- Y[2:length(Y)]
  Y0 <- Y[1:(length(Y)-1)]
  aux <- 1/sqrt(2*pi*sigma^2)*exp(-(Y1-mu-rho*Y0)^2/(2*sigma^2))
  L <- L * prod(aux)
  return(L)
}

Next define function rQ that draws from the (Gaussian) proposal distribution, as well as function Q, that computes \(Q_{\tilde{\boldsymbol\theta}|{\boldsymbol\theta}}(\tilde{\boldsymbol\theta},{\boldsymbol\theta})\):

rQ <- function(x,a){
  n <- length(x)
  y <- x + a * rnorm(n)
  return(y)}
Q <- function(y,x,a){
  q <- 1/sqrt(2*pi*a^2)*exp(-(y - x)^2/(2*a^2))
  return(prod(q))}

We consider Gaussian priors:

prior <- function(param,means_prior,stdv_prior){
  f <- 1/sqrt(2*pi*stdv_prior^2)*exp(-(param - 
                                         means_prior)^2/(2*stdv_prior^2))
  return(prod(f))}

Function p_tilde corresponds to \(f_{{\boldsymbol\theta},Y}\):

p_tilde <- function(param,Y,means_prior,stdv_prior){
  p <- likelihood(param,Y) * prior(param,means_prior,stdv_prior)
  return(p)}

We can now define function \(\alpha\) (Eq. (3.18)):

alpha <- function(y,x,means_prior,stdv_prior,a){
  aux <- p_tilde(y,Y,means_prior,stdv_prior)/
    p_tilde(x,Y,means_prior,stdv_prior) * Q(y,x,a)/Q(x,y,a)
  alpha_proba <- min(aux,1)
  return(alpha_proba)}

Now, all is set for us to write the MCMC function:

MCMC <- function(Y,means_prior,stdv_prior,a,N){
  x <- means_prior
  all_theta <- NULL
  count_accept <- 0
  for(i in 1:N){
    y <- rQ(x,a)
    alph <- alpha(y,x,means_prior,stdv_prior,a)
    #print(alph)
    u <- runif(1)
    if(u < alph){
      count_accept <- count_accept + 1
      x <- y}
    all_theta <- rbind(all_theta,x)}
  print(paste("Acceptance rate:",toString(round(count_accept/N,3))))
  return(all_theta)}

Specify the Gaussian priors:

true_values <- c(mu,log(rho/(1-rho)),log(sigma))
means_prior <- c(1,0,0) # as if we did not know the true values
stdv_prior <- rep(2,3)
resultMCMC <- MCMC(Y,means_prior,stdv_prior,a=.45,N=20000)

## [1] "Acceptance rate: 0.098"

par(mfrow=c(2,3))
for(i in 1:length(means_prior)){
  m <- means_prior[i]
  s <- stdv_prior[i]
  x <- seq(m-3*s,m+3*s,length.out = 100)
  par(mfg=c(1,i))
  aux <- density(resultMCMC[,i])
  par(plt=c(.15,.95,.15,.85))
  plot(x,dnorm(x,m,s),type="l",xlab="",ylab="",main=paste("Parameter",i),
       ylim=c(0,max(aux$y)))
  lines(aux$x,aux$y,col="red",lwd=2)
  abline(v=true_values[i],lty=2,col="blue")
  par(mfg=c(2,i))
  plot(resultMCMC[,i],1:length(resultMCMC[,i]),xlim=c(min(x),max(x)),
       type="l",xlab="",ylab="")}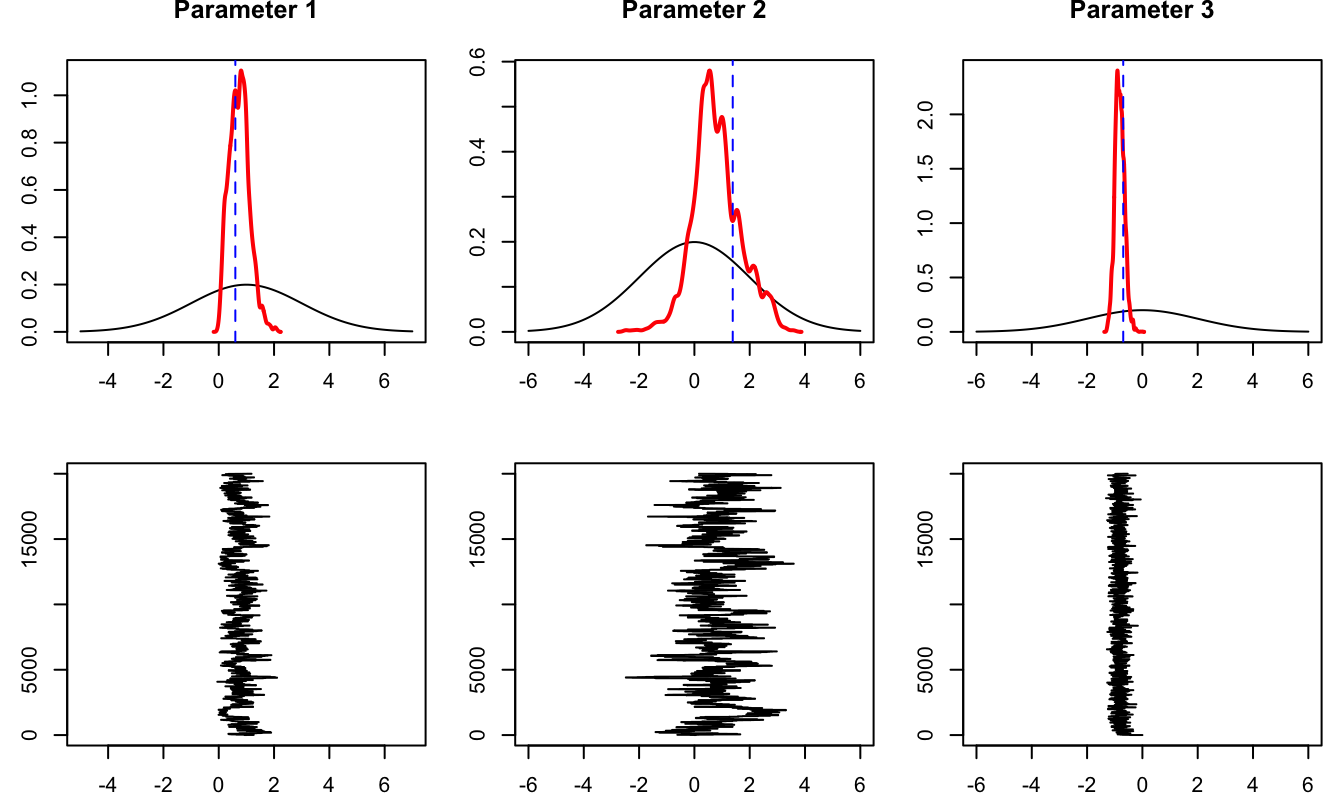

Figure 3.6: The upper line of plot compares prior (black) and posterior (red) distributions. The vertical dashed blue lines indicate the true values of the parameters. The second row of plots show the sequence of \(\boldsymbol\theta_i\)’s generated by the MCMC algorithm. These sequences are the ones used to produce the posterior distributions (red lines) in the upper plots.